前言

轮胎是汽车与外界环境相互作用最重要的部件。在中低速正常行驶时，轮胎力在所有汽车外界作用力中占主导地位，在高速正常行驶时，汽车所受空气作用力较大，但是空气作用力相对不可控，轮胎力仍是改变车辆运动状态的重要作用力。因此在底盘运动控制中，轮胎力的控制十分重要。并且无论是转向控制、驱制动控制，其本质都是改变轮胎力从而改变车辆运动状态。因此，准确地描述轮胎的纵侧向力，对底盘控制具有重要原因，特别是对非线性模型预测控制等带有预测的控制方法。

然而，轮胎具有强烈的非线性特性，在小滑移情况下，轮胎力与滑移大致呈现线性关系，在滑移较大时，轮胎力趋向饱和。因此，轮胎力不能直接简化为某个简单函数，轮胎力是一个关于滑移量的非线性函数，轮胎模型具有一定的研究与学习价值。

本文首先介绍轮胎模型的主要功能，其次介绍轮胎模型的分类与各种模型的适用场景，最后，为了论述的统一，介绍了ISO轮胎坐标系。

轮胎模型是什么

如下图所示。轮胎模型是研究轮胎与外界环境相互作用力的数学模型，用于描述轮胎在各种运行条件下所受到的力/力矩与输入变量之间关系。它是车辆动力学仿真和运动控制算法的核心部件，不准确的轮胎模型无法准确预测车辆行为。

轮胎模型

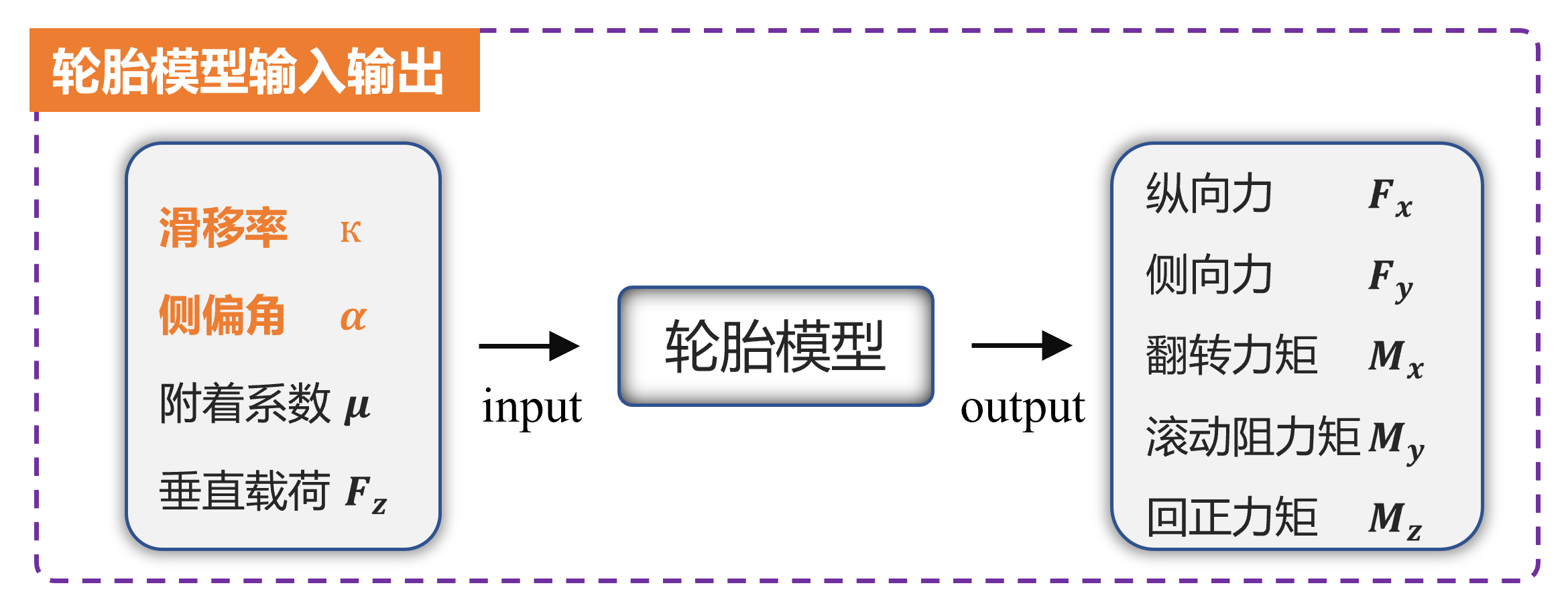
轮胎模型的核心任务就是建立输入与输出之间的数学映射关，它可以是数学公式，也可以是查表模型，或者是基于数据驱动的神经网络拟合模型等等。由于轮胎的橡胶黏滑特性、橡胶滞回、胶料温度老化以及速度依赖等问题，轮胎具有强烈的非线性特性，因此一般基于实验数据的拟合方法得到的轮胎建模具有较高的精度。其输入为滑移率$\kappa$、侧偏角$\alpha$、垂向载荷$F_z$、轮速$\omega$、侧向速度$v_y$，输出为轮胎产生的力矩$F_x$、$F_y$、$M_z$等等。

轮胎模型分类与适用场景

在车辆系统动力学的理论研究与工程实践中，轮胎模型的选择需要充分考虑研究目的以及使用需求。从建模思路出发，轮胎模型可分为理论物理模型、经验与半经验模型以及自适应动态模型三大范畴。

其中，理论物理模型的典型代表是刷子模型，它将轮胎胎面简化为一系列独立的弹性体刷毛，从接触力学的基本原理出发，推导轮胎力的产生机制。这类模型的最大优势在于其清晰的物理图像，能够直观地解释如摩擦椭圆、力饱和等基本现象，并且通常具有较少的待辨识参数。然而，其对于现代子午线轮胎复杂结构的简化，使得它在高精度拟合实测轮胎数据方面存在局限，因此多用于机理研究、教学阐释或作为更复杂模型的物理基础。

为了满足工程开发中对高预测精度的迫切需求，以Pacejka魔术公式为代表的经验与半经验模型成为了绝对的主流。这类模型没有深入研究轮胎的物理特性从而进行机理建模，而是通过三角函数等数学结构，对海量的轮胎台架试验数据进行高精度拟合，这与傅里叶级数有异曲同工之妙。这种模型具有显著的工程实用优势：在统一的数学框架下，通过调整大量系数，可以极为精确地复现轮胎在纵向、侧向、联合滑移乃至回正力矩等多方面的静态特性。因此，凭借其优异的模型拟合能力与可控的计算复杂度，该工具已成为车辆操纵稳定性分析、底盘控制系统开发及硬件在环仿真中的行业标准。

经典魔术公式主要用于描述稳态或准稳态条件下的轮胎力特性，但在涉及不平路面激励、高频操纵输入或车辆平顺性等问题时，轮胎的动态响应不可忽略。这一需求推动了自适应动态模型的发展，其核心是在半经验稳态模型基础上引入反映力生成滞后的“松弛长度”以及滚动包络效应。例如 MF-Swift 模型在魔术公式之上耦合刚性环结构，可有效模拟轮胎对路面不平输入的动态滤振行为及更高频率的力响应，使模型应用从传统操控分析扩展至耐久载荷预测、乘坐舒适性评估与高级底盘协同控制等领域。

在电动化与智能化背景下，面对轮边电机高精度扭矩控制与极端工况稳定性边界探索等新挑战，轮胎模型的研究正向更高的集成度与更高的保真度演进。一方面，模型开始深度嵌入热力学机制，以刻画激烈驾驶导致的胎温变化对抓地力的影响；另一方面，基于有限元与多体动力学的高精度数字轮胎模型迅速发展，尽管计算成本较高，但能够在研发阶段预测结构设计、材料参数与胎压设置对性能的影响。总体来看，轮胎模型的分类体系仍在不断拓展，其演进逻辑始终围绕在“物理真实性”“计算效率”与“场景适配性”之间寻求最优平衡。模型的选择本质上是一种基于仿真目标、精度需求与资源约束的关键性权衡，没有通用答案，唯有深入理解模型机理与问题边界，才能确定最契合的技术路径。

One more

轮胎坐标系

毫无疑问，在车辆动力学与轮胎力学的建模与分析中，明确一个参考坐标系是十分必要的，否则在后续的工作中难免产生混乱与错误。国际上存在两套广泛使用且具有权威性的轮胎坐标系标准：一套由美国汽车工程师学会制定（SAE），另一套由国际标准化组织颁布（ISO）。

SAE 坐标系（SAE J670）广泛应用于北美汽车工业及传统车辆动力学教材。该坐标系的 $Z$ 轴垂直向下，$X$ 轴指向车辆前进方向。$Z$ 轴指向地面，使重力加速度方向与 $Z$ 轴正向一致，便于描述垂向载荷。在该体系下，$Y$ 轴根据右手法则指向驾驶员右侧，因此车辆右转的侧向加速度为正，而地面对轮胎的垂直支持力通常呈负值。

相较而言，ISO 坐标系（ISO 8855）更常被欧洲车企、多体动力学软件及现代控制研究采用。该体系同样规定 $X$ 轴指向前方，但将 $Z$ 轴正方向定义为竖直向上，更符合数学坐标系直觉。在此定义下，地面支持力为正值，而重力加速度沿 $Z$ 轴负方向。由于 $Y$ 轴指向驾驶员左侧，车辆左转时的横摆角速度与侧向运动被视为正值，与 SAE 坐标系呈现符号相反的关系。《汽车理论》清华/同济版均采用该方案。 如下图所示。

轮胎坐标系[汽车理论余志生]

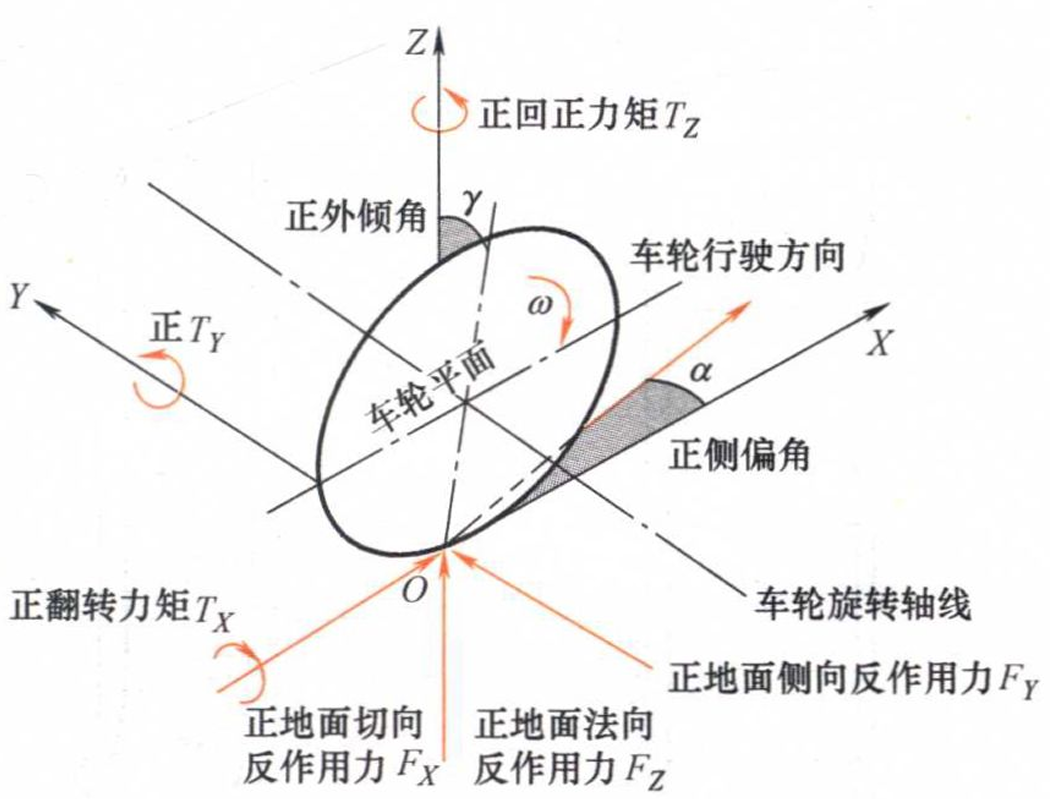
这两套标准在符号约定上的差异容易引发建模与仿真混乱，尤其是在处理侧偏角及回正力矩时更为显著。因此，在编写轮胎模型代码、调用 .tir 文件或进行联合仿真前，必须确认所使用的基准坐标系。忽略符号统一或转换往往会导致“反向转向”或模型发散，这是最常见的仿真错误之一。

Calibrated

版权所有

版权归属：Duangce

许可证：署名 4.0 国际 (CC-BY-4.0)