轮胎模型-程序
约 2241 字大约 7 分钟
2025-11-24
前言
在上一节 轮胎数学模型 中,建立了魔术公式轮胎模型的数学模型。本节将付诸实践,从某轮胎的测试数据出发,介绍如何得到描述该轮胎特性的魔术公式。本节首先对数据进行拟合得到魔术公式的相关参数,其次构建函数,最后绘制不同情况的轮胎力响应曲线。
Problem statement
首先我们将上一节得到的就算轮胎力的魔术公式轮胎模型摘抄在下面:
σx=1+κκσy=1+κtanασ∗=σx2+σy2(1)
⎩⎨⎧Fx=σ∗σxμFzξxsin[Cx0arctan{Bx0σ∗/μ−Ex0(Bx0σ∗/μ−arctanBx0σ∗/μ)}]Fy=σ∗σyμFzξysin[Cy0arctan{By0σ∗/μ−Ey0(By0σ∗/μ−arctanBy0σ∗/μ)}](2)
从公式 (1)(2) 可以看到,轮胎模型中不存在微积分操作,因此即使是在 simulink 中也无需像 转向系统模型 一样使用 Integral 模块进行积分,在 simulink 中也可以完全可以仅使用 matlab function 进行建模。
该模型的输入与输出等相关量整理在下表中:
| 输入参数 | 输出参数 | 内部量 |
|---|---|---|
| κ | Fx | ξx,y |
| α | Fy | Cx0,y0 |
| μ | Bx0,y0 | |
| Fz | Ex0,y0 |
当我们在脚本中搭建好轮胎模型,也就是将上述公式转为代码并构建函数后,只要将4个输入量全部输入到模型中,即可计算出对应的轮胎力。并且注意输入量的单位,务必确认输入量 α 的单位为国标 rad。
但是当我们真正着手开始建立模型时就会发现一个问题:该模型中的重要参数,即 “内部量” ξx,y 等等 ,该如何确定。这是搭建该模型最重要的第一个环节:确定拟合曲线的参数。
确定拟合曲线的参数
魔术公式是对轮胎测试数据的拟合,发明者告诉我们可以使用这样形式的公式,在大部分工况下准确地描述轮胎特性。然而,不同的轮胎具有不同的特性,其拟合参数也是不相同的。本小节将介绍,基于一个具体的轮胎测试数据,使用最小二乘法确实拟合曲线参数的过程。
最小二乘法(Least Squares Method, LSM)及其变种在曲线拟合方面具有优异的性能。其优势在于严谨的数学基础与良好的统计特性。在满足高斯-马尔可夫定理的假设下,该方法能够提供线性无偏估计中方差最小的最优解,并且其计算过程是具有明确解析解形式的,结果稳定且唯一。
LSM 的核心原理在于通过最小化残差平方和来确定模型的最优参数。对于给定的一组观测数据,LSM 将预测值与实际观测值之间残差的平方和作为损失函数,通过求解该损失函数关于模型参数的偏导数并令其为零,从而得到使拟合误差达到最小的参数估计值。这一过程在几何上可解释为在向量空间中寻找数据点的最佳逼近投影。
本节对MF的参数进行标定,使用的方法为非线性最小二乘法,标定的完整流程为:获取并整理数据、曲线拟合及参数辨识、确定参数。
(A) 首先是获取参数,有条件及需要则可以通过实验测量得到真实的数据,本小节从Carsim中得到这些轮胎数据。如下图所示,它们在整车模型->轮胎模型->轮胎力数据中,可以直接得到轮胎力与纵向滑移率、侧偏角的数据表。
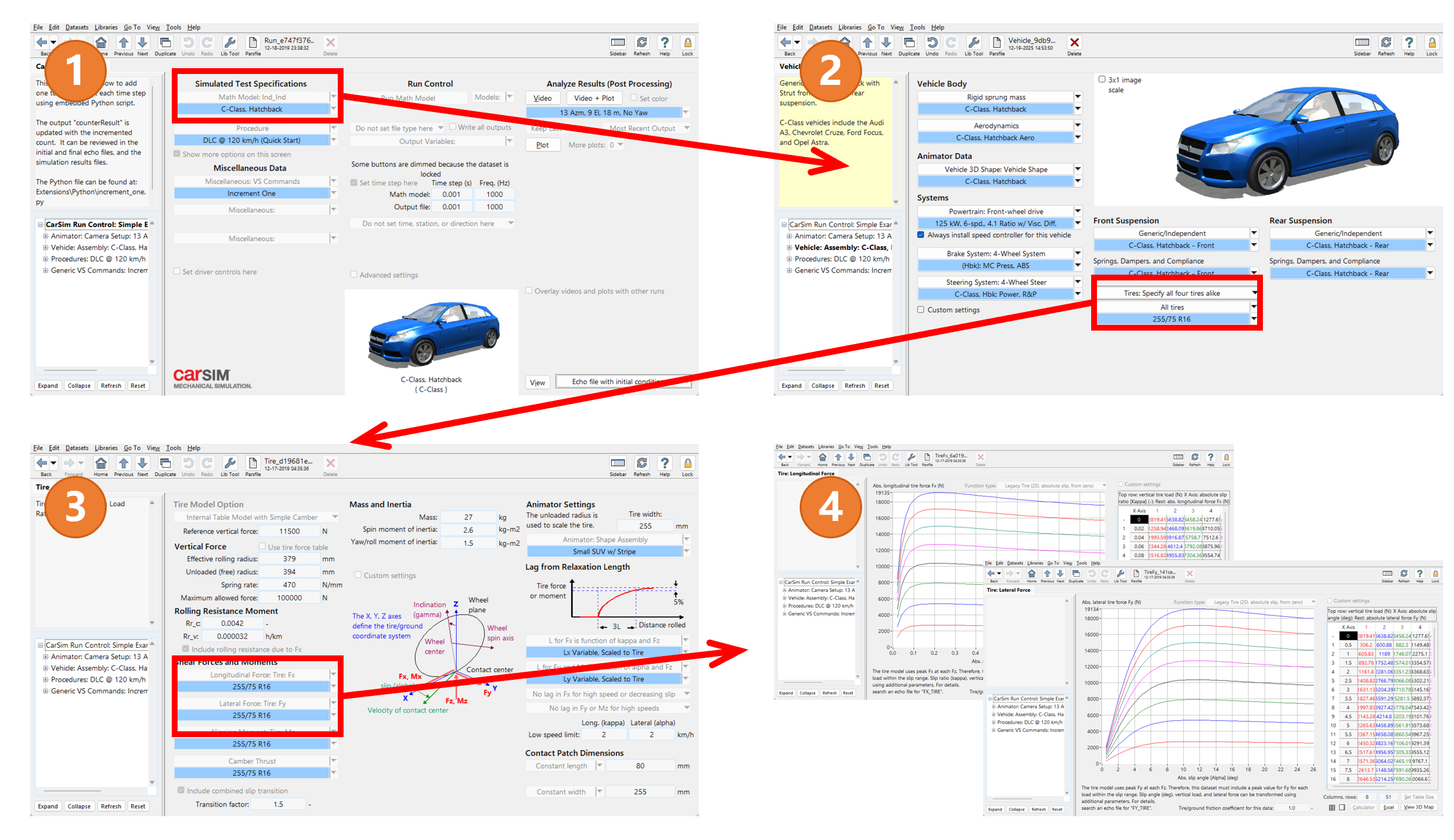
(B) 其次在 matlab 中使用拟合工具函数 fit 进行拟合:第一步读取数据,第二步进行拟合设置,第三步进行拟合。
在拟合前,注意到CarSim的轮胎数据是在纯纵/侧向滑移、轮胎路面摩擦系数为1 的条件下得到的,即分别对于 Fx,Fy 的计算式,它们的等效滑移率 σ∗ 分别为 σx,σy,并且 μ=1。由此将组合滑移工况的魔术公式 (2) 退化为纯滑移的魔术公式如下:
⎩⎨⎧Fx=Fzξxsin[Cx0arctan{Bx0σx−Ex0(Bx0σx−arctanBx0σx)}]Fy=Fzξysin[Cy0arctan{By0σy−Ey0(By0σy−arctanBy0σy)}](3)
第二三步代码如下图所示:

得到结果如下图所示,将结果带回原公式,则可以得到相应的魔术公式轮胎模型。

轮胎模型代码及简单测试
在得到魔术公式轮胎模型的参数后,便可以直接根据公式写出轮胎模型的计算函数,以 matlab 为例,其代码如下:
function [Fx,Fy] = tire_force_cal(kappa, alpha, Fz, mu)
% kappa-纵向滑移率; alpha-侧偏角; mu-附着系数; Fz-垂向载荷
% 组合滑移率计算 (combined slip theory)
sigma_x = -kappa./(1+kappa);
sigma_y = tan(alpha)./(1+kappa);
sigma_t = sqrt(sigma_x.^2+sigma_y.^2);
% 拟合的纵、侧向轮胎力魔术公式
Fx0 = mu*Fz.*0.9022.*sin(1.399*atan(18.01*(1-0.698)*(sigma_t./mu)+0.698*atan(18.01*(sigma_t./mu))));
Fy0 = mu*Fz.*0.9028.*sin(2.243*atan(5.711*(1-1.023)*(sigma_t./mu)+1.023*atan(5.711*(sigma_t./mu))));
Fx = Fx0.*sigma_x./sigma_t;
Fy =-Fy0.*sigma_y./sigma_t;
end只需要输入相应的纵向滑移率、侧偏角、轮胎路面摩擦系数、垂向力,即可计算一个轮胎的纵侧向力。 至此,魔术公式轮胎模型建立完成。通过输入不同的纵侧向滑移,可以绘制 1.纯纵滑纵向力 2.纯侧偏侧向力 3.组合滑移纵向力 4.组合滑移侧向力 四个图像,如下所示:
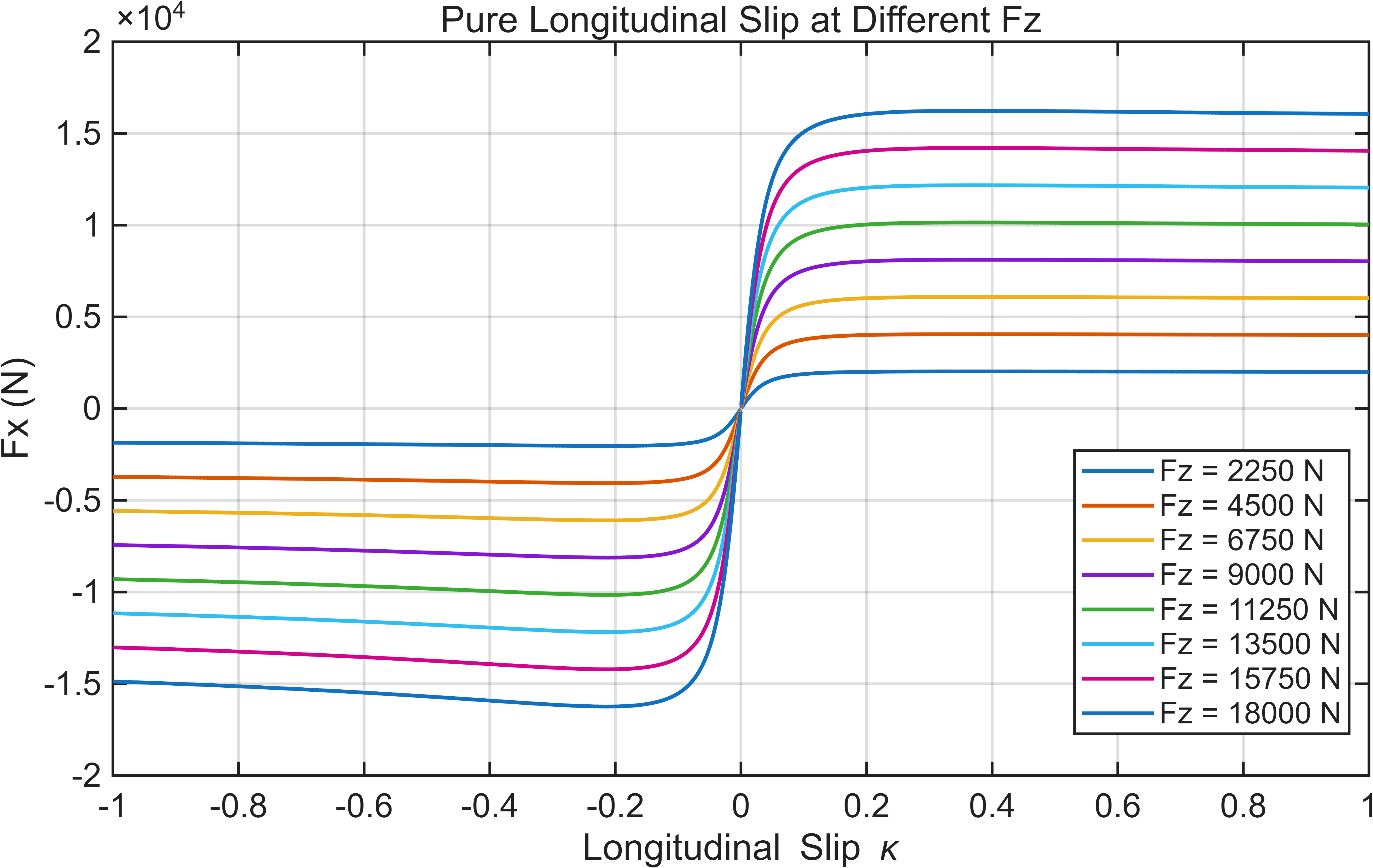
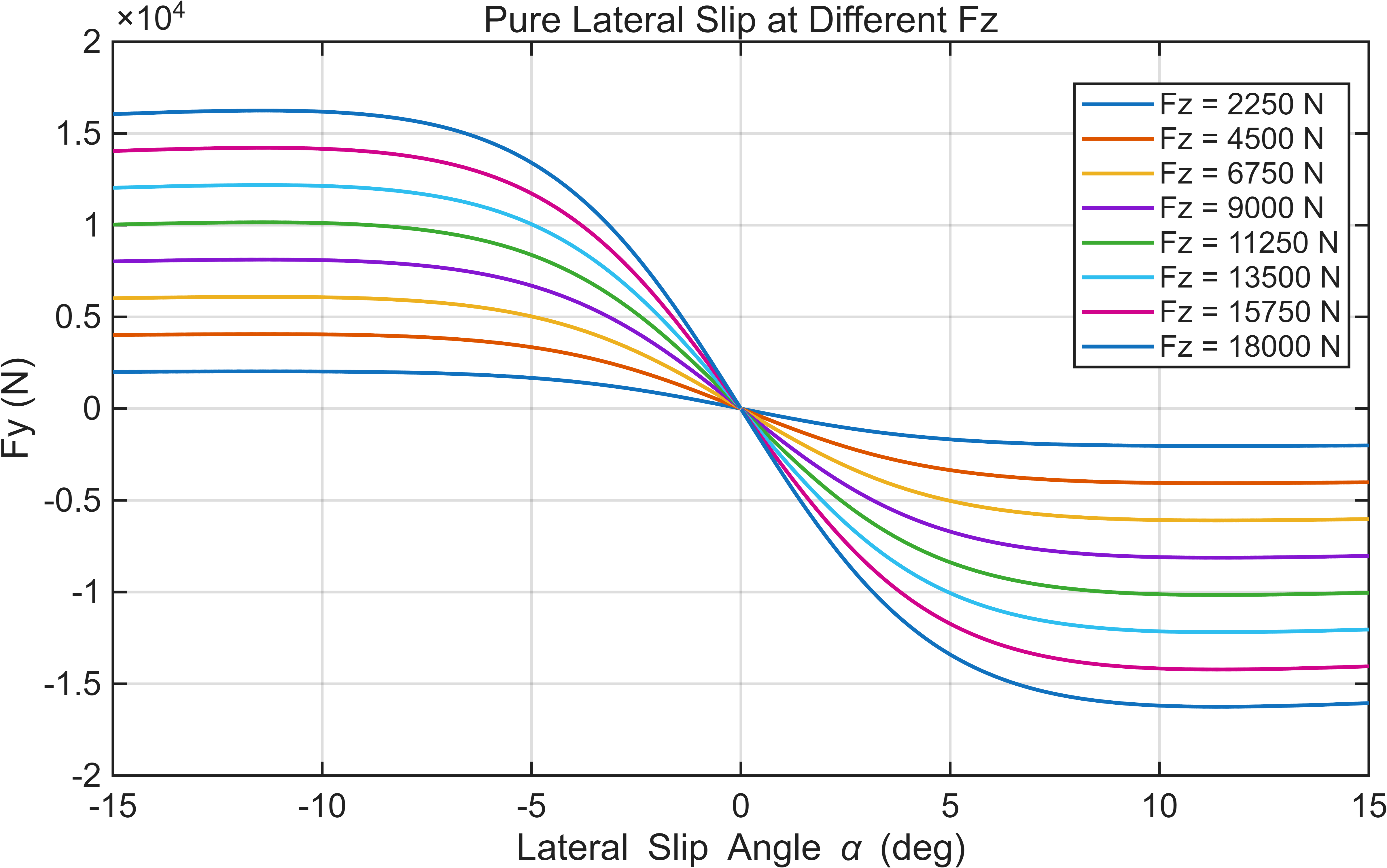
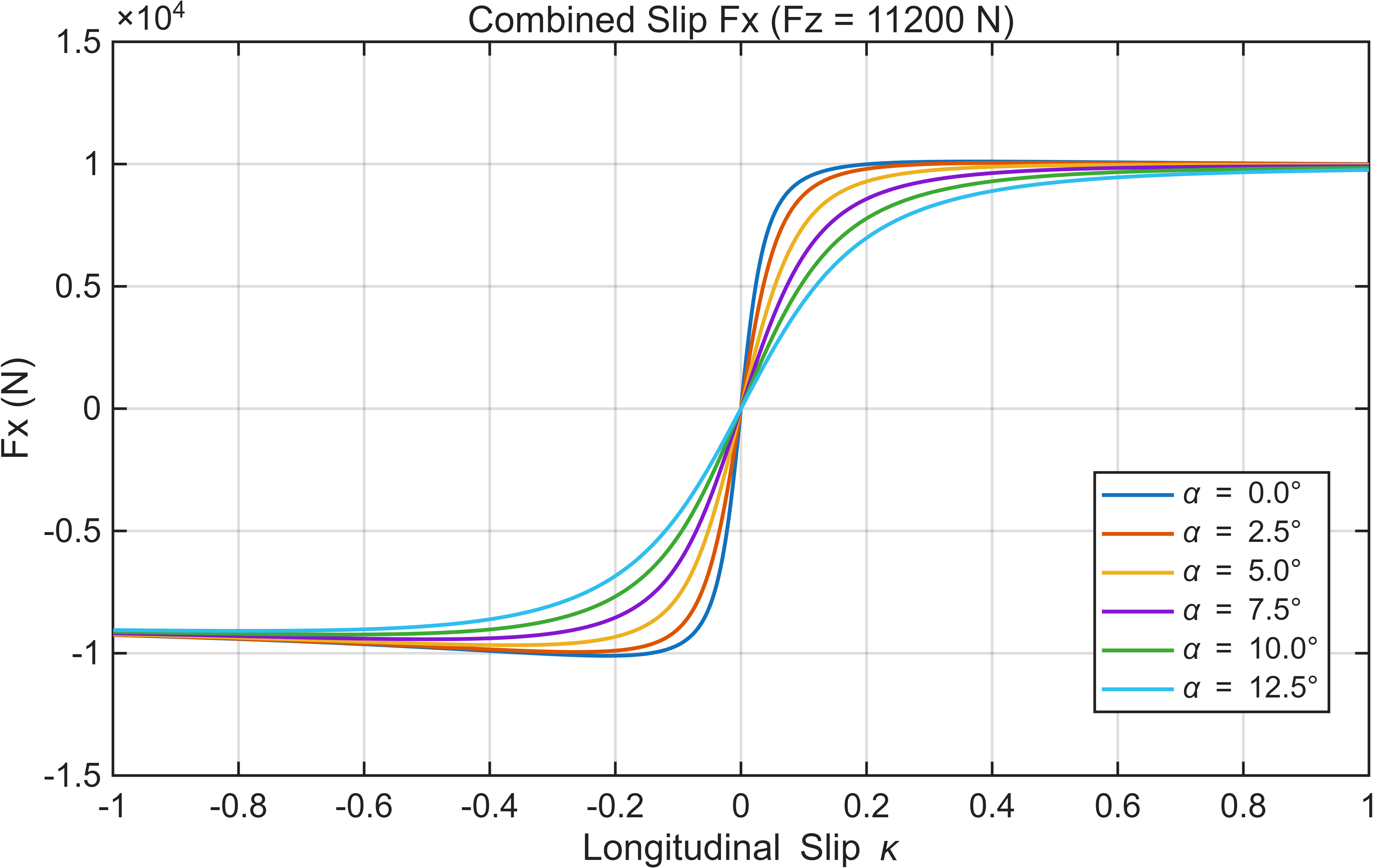
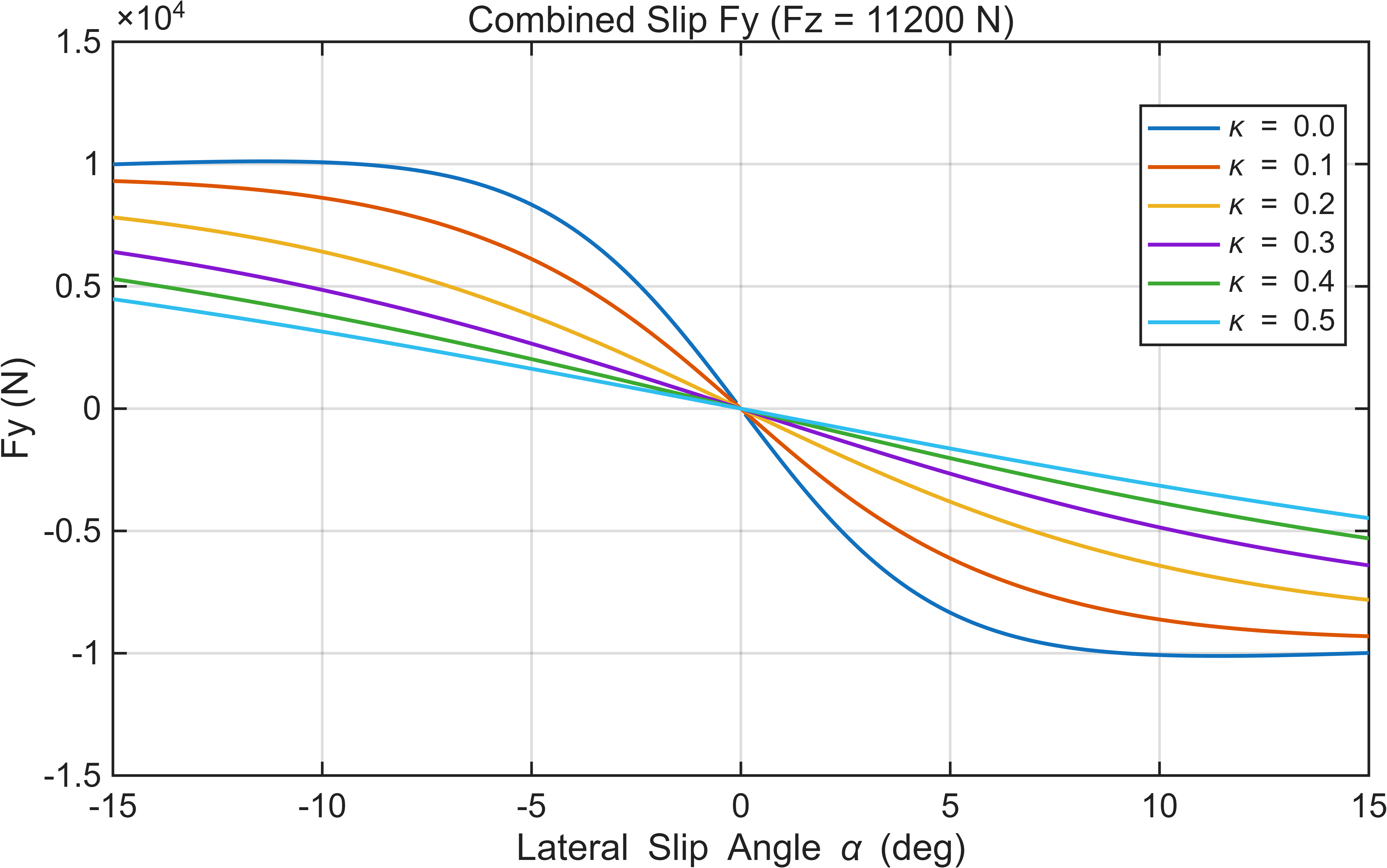
more over
本文使用的 魔术公式+组合滑移 的计算方法其实做了一定的简化,但是足以应对面向一般工况(非爆胎等)的轮胎控制与建模。更多详细深入的内容可以参考专业书籍 Tyre and Vehicle Dynamics, Hans B. Pacejka.
其次,本文也同样给出轮胎模型的 python 版本:
def force_wheel(kappa, alpha, F_z, mu):
"""
kappa: 纵向滑移率 ndarray (4,) 1
alpha: 侧偏角 ndarray (4,) rad
F_z: 垂向力 ndarray (4,) N
mu: 轮胎路面摩擦系数 ndarray(4,) 1
"""
sigma_x = kappa / (1 + kappa)
sigma_y = np.tan(alpha) / (1 + kappa)
sigma_t = np.sqrt(sigma_x**2 + sigma_y**2) + 1e-12
# Fx0, Fy0 per Magic formula
Fx0 = mu * F_z * 0.9022 * np.sin(
1.399 * np.arctan(18.01 * (1 - 0.698) * (sigma_t / mu) + 0.698 * np.arctan(18.01 * (sigma_t / mu)))
)
Fy0 = mu * F_z * 0.9028 * np.sin(
2.243 * np.arctan(5.711 * (1 - 1.023) * (sigma_t / mu) + 1.023 * np.arctan(5.711 * (sigma_t / mu)))
)
F_x = (sigma_x / sigma_t) * Fx0
F_y = - (sigma_y / sigma_t) * Fy0
return F_x, F_y
此外,关于 该模型的输入 κ,α,Fz 等可以直接作为已知量输入,但是实际情况是,在车辆运行过程中,没有直接测量这些输入的传感器,而是需要通过其他车辆参数与状态进行计算的。对于如何通过整车状态进行计算,可以参考专业课书籍《汽车理论》或者通过网络搜索。这部分内容与轮胎模型的主题有很强的相关性,但一般不算做轮胎模型的一部分,因此如果有机会,后续将添加这部分内容 (now is 251207)。
致谢
感谢师兄陈俊成,本节的 m脚本 脱胎于他的相关项目,通过学习他的项目,结合相关专业书籍、CarSim说明文档,我迅速掌握了相关知识,并顺利完成本节内容。
Calibrated
