一、2DOF 模型的意义与应用

描述车辆质心侧偏角、横摆角速度的线性二自由度模型（下称“2-DOF 模型”）是车辆横向动力学中最基础、最常用的线性化模型之一。

其工程意义体现在三方面：第一，它把车辆的横向稳定性与指向性的核心动作（侧偏与横摆）提炼到两个状态，便于分析操稳极限、临界速度、转向不足/过度等现象；第二，它是控制器设计（如横向路径跟踪、车道保持、稳定性控制器 ESP/ESC ）中常用的被控对象与线性化基准，许多线性控制方法（LQR、频域设计、增益调度）都基于该模型或其线性化形式；第三，它在快速整车仿真、参数辨识（轮胎侧偏刚度）和教学中提供了直观的物理解释与数学便利性。

其典型应用包括：稳定性分析（临界速度、临界侧偏刚度比）、控制器设计与验证、快速仿真与参数灵敏度分析、以及作为更高阶模型（例如 7-DOF、14-DOF）线性化的基线模型。

二、物理设定与符号

为保证推导清晰，须首先给出物理设定与符号约定，车辆坐标系为上一节 整车模型概述 中提到的 ISO 车辆坐标系，此处提炼出来给出符号速查表如下：

符号	含义与单位
$m$	车辆质量（kg）
$I_z$	绕垂直轴转动惯量（kg·m²）
$l_f, l_r$	前/后轴到质心的距离（m）
$C_f, C_r$	前/后轮侧向刚度（N/rad）
$V_x$	车辆前进速度（m/s），在本模型中通常视为常数
$\beta$	质心侧偏角（rad），$\beta \approx v_y / V_x$
$r$	横摆角速度（rad/s）
$\delta$	前轮转角（rad）
$F_{yf}, F_{yr}$	前/后轮侧向力（N）

三、逐步推导微分方程组

建模思路： 根据牛顿-欧拉公式，首先建立车辆刚体横向动力学与横摆动力学平衡方程；其次把线性轮胎力表达为侧偏角的线性函数；再次，利用速度—角速度与侧偏角的关系，把所有变量写成 $\beta, r$（以及控制量 $\delta$、常速 $V_x$）的方程，最后整理得到状态空间形式。

1. 刚体动力学基础方程（平面运动）

车辆单轨模型如下图所示：

图 1 整车单轨模型

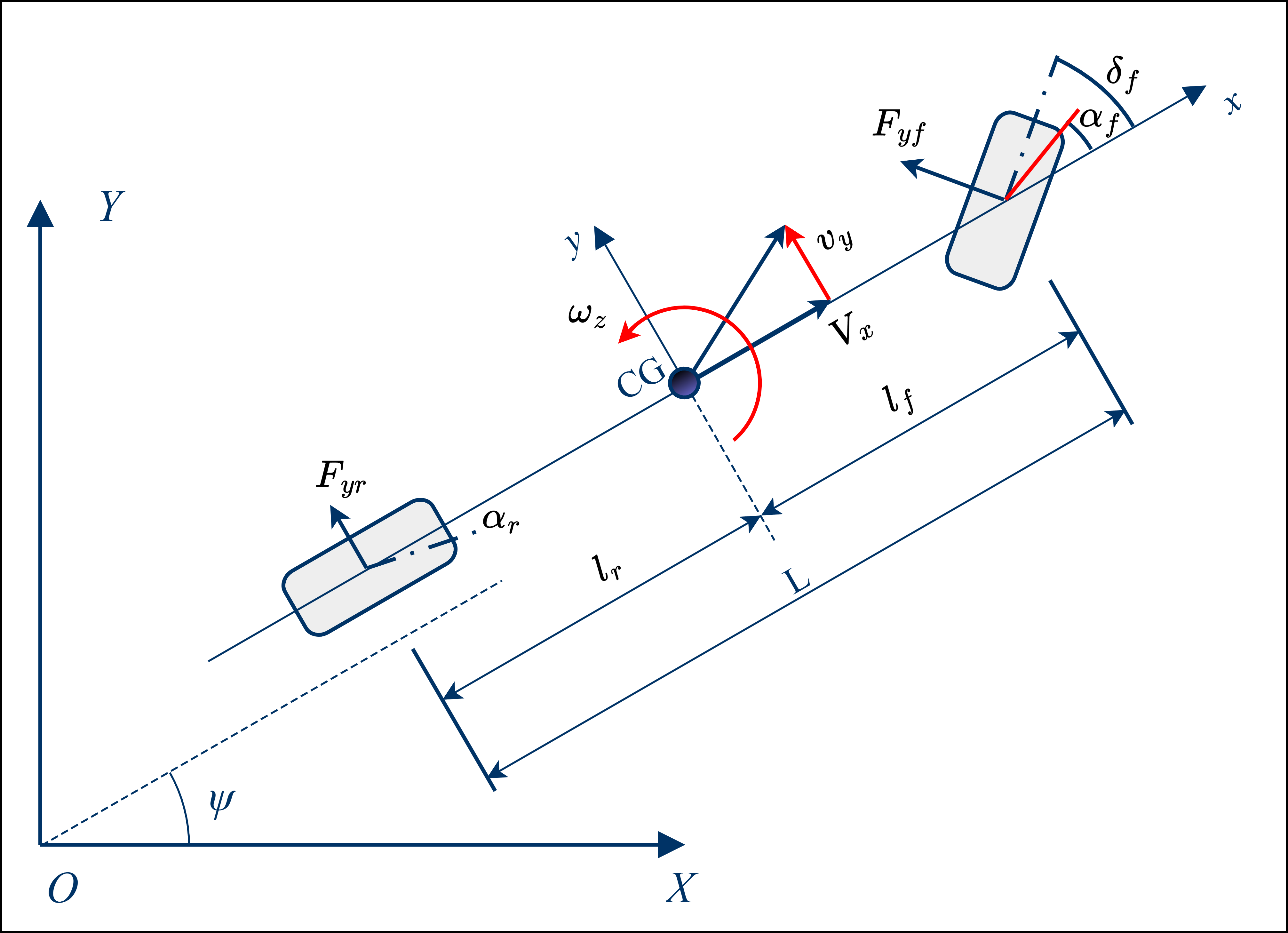
根据该图，可以列出如下的平衡方程，

(A) 车辆在平面上的横向动力学（横向平移）的平衡方程为

$$m a_y = F_{yf} + F_{yr}, \tag{1}$$

其中，$m$ 为整车质量，$a_y$ 为侧向加速度，$F_{yf},F_{yr}$ 分别表示前后轮侧向力。

(B) 横摆动力学（转矩平衡）为

$$I_z \dot{r} = l_f F_{yf} - l_r F_{yr}. \tag{2}$$

其中，$I_z$ 为整车绕 $z$ 轴的转动惯量，$r$ 为车辆横摆角速度，$l_f,l_r$ 分别代表前/后轴到质心的纵向距离。

这两式是刚体动力学的直接写法，注意力矩臂的符号约定（前轮产生正矩 $l_f F_{yf}$，后轮产生负矩 $-l_r F_{yr}$）。

2. 关联侧向速度加速度 $v_y, a_y$ 与侧偏角 $\beta$

车辆的侧向加速度$a_y$与侧向速度的导数$\dot{v}_y$并不是简单的微积分关系，其关系如下

$$a_y = \dot{v}_y + v_x r$$

其中，$v_x r$ 是由于车辆坐标系旋转而产生的侧向变化量分量。车辆侧向加速度之所以不是 $\dot{v}_y$，就是因为在车体这种旋转的非惯性系中求导会出现类似科氏加速度的附加项。详细推导请见 整车不得不说的。

质心侧偏角定义为 $\beta = \arctan(v_y /v_x)$。在侧偏角较小时，可以使用小角度近似 $\arctan(x)\approx x$，则 $\beta \approx v_y / v_x$。由此，在 $v_x=V_x$ 为常数时可以得到

$$v_y \approx V_x \beta, \quad \dot{v}_y \approx V_x \dot{\beta}.$$

将其代入横向平动方程，并直接将左侧公因式 $V_x$ 提至括号外，可以得到

$$mV_x(\dot{\beta} + r) = F_{yf} + F_{yr}. \tag{3}$$

Note that: 这一步清楚体现了质心侧偏角变化率与横摆角速度的潜在相互影响关系。

3. 轮胎力线性近似

参考 轮胎:合纵连横 中对于轮胎侧偏角的相关计算，对前后轮侧偏角做小角近似。前后轮侧偏角可以表示为：

$\alpha_f \approx \beta + \frac{l_f}{V_x} r - \delta.$

$\alpha_r \approx \beta - \frac{l_r}{V_x} r.$

此时，车辆为前轮转向汽车，无主动后轮转向功能。并且两式中 $\beta$ 为质心侧偏角；项 $\frac{l_f}{V_x} r$ 与 $\frac{l_r}{V_x} r$ 来自于横摆速度在轮心处对速度方向的贡献（即 $v_{yw} = v_y + l_f r$ 的线性化）。

在线性轮胎模型中，前后轮侧向力为

$$\begin{aligned} F_{yf} &= C_f \alpha_f = C_f \left( \beta + \frac{l_f}{V_x} r -\delta \right),\\ F_{yr} &= C_r \alpha_r = C_r \left( \beta - \frac{l_r}{V_x} r \right). \tag{4} \end{aligned}$$

由此，轮胎力被描述为关于横摆角速度、质心侧偏角、前轮转角的线性函数。

4. 代回侧向与横摆方程

首先，将 $F_{yf}$、$F_{yr}$ 代入横向平动方程：

$mV_x(\dot{\beta} + r) = C_f \left( \beta + \frac{l_f}{V_x} r -\delta \right)+ C_r \left( \beta - \frac{l_r}{V_x} r \right) .$

把同类项整理得到：

$mV_x \dot{\beta} + mV_x r = (C_f + C_r) \beta + \left( C_f \frac{l_f}{V_x} - C_r \frac{l_r}{V_x} \right) r -C_f \delta.$

将项移到左侧并除以 $mV_x$：

$$\dot{\beta} = \frac{C_f + C_r}{mV_x} \beta + \left( \frac{C_f l_f - C_r l_r}{m V_x^2} - 1 \right) r - \frac{C_f}{mV_x} \delta. \tag{5}$$

其次，对横摆方程代入：

$I_z \dot{r} = l_f F_{yf} - l_r F_{yr} = l_f C_f \left( \beta + \frac{l_f}{V_x} r -\delta \right) - l_r C_r \left( \beta - \frac{l_r}{V_x} r \right).$

展开并整理：

$I_z \dot{r} = (l_f C_f - l_r C_r) \beta + \left( \frac{l_f^2 C_f + l_r^2 C_r}{V_x} \right) r - l_f C_f \delta .$

将右端项带到左并除以 $I_z$，整理为标准形式：

$$\dot{r} = \frac{l_f C_f - l_r C_r}{I_z} \beta + \frac{l_f^2 C_f + l_r^2 C_r}{I_z V_x} r - \frac{l_f C_f}{I_z} \delta.\tag{6}$$

5. 矩阵形式

在上小节“代回侧向与横摆方程”中，线性二自由度动力学模型被描述为

$$\begin{cases} \dot{\beta} = \frac{C_f + C_r}{mV_x} \beta + \left( \frac{C_f l_f - C_r l_r}{m V_x^2} - 1 \right) r - \frac{C_f}{mV_x} \delta, \\ \dot{r} = \frac{l_f C_f - l_r C_r}{I_z} \beta + \frac{l_f^2 C_f + l_r^2 C_r}{I_z V_x} r - \frac{l_f C_f}{I_z} \delta, \end{cases} \tag{7}$$

令状态向量 $\boldsymbol{x} = [\beta \quad r]^T$，控制量为前轮转向角 $\delta$，则线性二自由度模型可被整理为

$$\begin{bmatrix} \dot{\beta} \\ \dot{r} \end{bmatrix} = \underbrace{ \begin{bmatrix} \dfrac{C_f + C_r}{mV_x} & \dfrac{C_f l_f - C_r l_r}{mV_x^2} - 1 \\ \dfrac{C_f l_f - C_r l_r}{I_z} & \dfrac{C_f l_f^2 + C_r l_r^2}{I_z V_x} \end{bmatrix} }_{\boldsymbol{A}} \begin{bmatrix} \beta \\ r \end{bmatrix} + \underbrace{ \begin{bmatrix} -\dfrac{C_f}{mV_x} \\ -\dfrac{C_f l_f}{I_z} \end{bmatrix} }_{\boldsymbol{B}} \delta.$$

注意矩阵中含有车辆前进速度 $V_x$，因此矩阵 $\boldsymbol{A}, \boldsymbol{B}$ 关于工况速度是参数化的（即为参数依赖的线性模型）；在控制和分析中常在给定工作点 $V_x = {V_x}_0$ 下固定矩阵进行设计。

四、建模假设

模型是对复杂客体的模拟，针对不同的需求，必然做出一定的简化，简化则导致精度下降以及适用条件收缩，为保证模型在使用过程中的有效性，必须使其在规定的范围内运行，该范围的界定依据为我们建立模型时所作的假设，当仿真出现问题时，首先考虑是否超出预设范围。

部分假设其实已在推导过程中给出，但是还有一些假设是没有直接提到但是必须明确的。因此，总结假设如下，以便查阅：

1. 平面刚体假定：车辆仅在水平平面运动（忽略纵向、垂向/翻滚/俯仰动力学与轮胎竖向运动）。
2. 常速假定/纵向动力学分离：车辆纵向速度 $V_x$ 假设为给定常数（或慢变化以致可视为常数），忽略纵向加速度对横向动力学的耦合。若要包含加速/制动的纵向载荷转移，需要额外项。
3. 小角度与线性化假定：侧偏角 $\beta$、前轮转角 $\delta$、侧偏角近似 $\tan \alpha \approx \alpha$、$\beta \approx v_y / V_x$ 等均采用一阶近似，因而模型为线性。
4. 轮胎线性且未饱和：轮胎侧向力与侧偏角呈线性关系 $F_y = -C \alpha$。只在轮胎线性工作区（小侧偏）近似成立；不考虑轮胎在大侧偏/大滑移下的饱和与摩擦极限约束（需要组合滑移模型、摩擦椭圆等处理）。
5. 忽视悬架影响与载荷转移：未考虑侧倾引起的载荷转移、非对称载荷分布、轮胎垂向力变化对 $C_f, C_r$ 的依赖（若需要，应将 $C$ 做 $F_z$ 依赖化）。
6. 对称车辆：左右对称，前/后轴仅按轴分布参数，不考虑左右不对称性、前后差异化动态耦合（除 $l_f, l_r, C_f, C_r$ 已区分）。

这些假设共同决定了该模型在小扰动、未饱和、平路工况附近最为可靠；偏离这些条件时模型可能失真。

五、结语

线性二自由度模型以其明确的物理解释与数学简洁性，在车辆动力学、控制与教学中占据基础而重要的位置。它既能作为快速设计与分析工具，也能为更高阶、非线性模型提供线性化基准。使用时要清楚其假设边界：恒定速度、小侧偏、线性轮胎区间、忽略载荷转移与轮胎瞬态动力学。

结语之外 — 四轮转向

🚛 目前（11/12/25）主动后轮转向技术已不再是高端豪华品牌车辆的专属，国内外零部件供应商的相关研究、设计、生产等也逐渐趋向成熟，并且已有30万内的量产车配备了相关技术。

并且，更reasonable的是笔者的研究包括四轮转向控制。因此，本小节给出四轮转向的二自由度动力学模型。

前轮转向汽车与四轮转向汽车在侧向动力学方面主要的区别是后轮侧向力$F_{yr}$，在线性轮胎模型中，其区别体现在后轮侧偏角。参考前轮侧偏角的计算式，在有后轮转向时的后轮侧偏角为

$$\alpha_r = C_r \left( \beta - \dfrac{l_r}{V_x}r - \delta_r\right),$$

其中，$\delta_r$为后轮转角。

由此，将新的$\alpha_r$代入原轮胎力公式 (4) ，并且结合侧向和横摆运动的公式 (3)(2)，同时将其中的前轮转角符号$\delta$替换为$\delta_f$，则可得到四轮转向汽车的线性二自由度动力学模型

$$\begin{cases} \dot{\beta} = \frac{C_f + C_r}{mV_x} \beta + \left( \frac{C_f l_f - C_r l_r}{m V_x^2} - 1 \right) r - \frac{C_f}{mV_x} \delta_f - \frac{C_r}{mV_x} \delta_r, \\ \dot{r} = \frac{l_f C_f - l_r C_r}{I_z} \beta + \frac{l_f^2 C_f + l_r^2 C_r}{I_z V_x} r - \frac{l_f C_f}{I_z} \delta_f + \frac{l_rC_r}{I_z}\delta_r. \end{cases}$$

Calibrated

版权所有

版权归属：Duangce

许可证：署名 4.0 国际 (CC-BY-4.0)