在上一节 轮胎模型概述 中我们已经论述了轮胎模型的分类，包括理论物理模型、经验与半经验模型、自适应动态模型三大类，并已阐明：魔术公式（Magic Formula, MF）轮胎模型在工程实践中具有广泛的研究与应用。

因此，本节重点对 MF 展开论述，首先直接给出 MF 的具体形式并介绍其部分内涵；其次论述相似性原理，基于该方法可以仅使用一组公式参数应对实际复杂多变的工况；最后介绍组合滑移理论，用以处理轮胎纵侧向同时滑移时的复杂工况。

魔术公式 Magic Formula

魔术公式由荷兰 Delft 工业大学的 H.B. Pacejka教授及其团队于1980年代至1990年代系统性地提出并完善。其 Magic 之处在于能够使用统一的数学结构，拟合出精确的纵向力、侧向力、回正力矩等轮胎力而无需物理原理支撑。对于给定的垂直载荷和外倾角值，其统一公式为：

$$y = D \sin [C \arctan\{Bx-E(Bx-\arctan Bx)\}] \tag{1}$$

并且为处理轮胎的不对称、非理想特性，对横纵向坐标的偏移进行一定补偿，更新计算式如下：

$$\begin{aligned} &Y(X) = y(x) + S_V \\ &x = X + S_H \end{aligned} \tag{2}$$

其中：

$$\begin{aligned} & Y: \text{输出量，包括}\quad F_x, F_y, M_z \\ & X: \text{输入量，包括}\quad \kappa,\tan\alpha \end{aligned}$$

并且：

$$\begin{aligned} &B\qquad\text{刚度因子} \\ &C\qquad\text{形状因子} \\ &D\qquad\text{峰值} \\ &E\qquad\text{曲率因子} \\ &S_H\quad\ \text{水平位移} \\ &S_V\quad\ \text{垂直位移} \\ \end{aligned}$$

魔术公式 $y(x)$ 通常产生一条曲线，经过原点 $x = y = 0$，达到最大值，随后趋于水平渐近线。对于给定的系数 $B,C,D$ 和 $E$，曲线关于原点呈反对称形状。为了使曲线相对于原点发生偏移以对准轮胎试验数据，引入了两个位移 $S_H$ 和 $S_V$。由此产生一组新的坐标 $Y(X)$。

该公式能够生成与测量曲线高度吻合的特性曲线，适用于侧向力 $F_y$（若需要也可用于对中扭矩 $M_z$）以及纵向力 $F_x$，这些力均作为其对应滑移量（滑移角 $\alpha$和纵向滑移 $\kappa$）的函数呈现。并且参数中已包含纵向载荷 $F_z$ 和轮胎外倾角 $\gamma$ 的影响。

由原始正弦版本的魔术公式产生的曲线 [Tyre and vehicle dynamic]

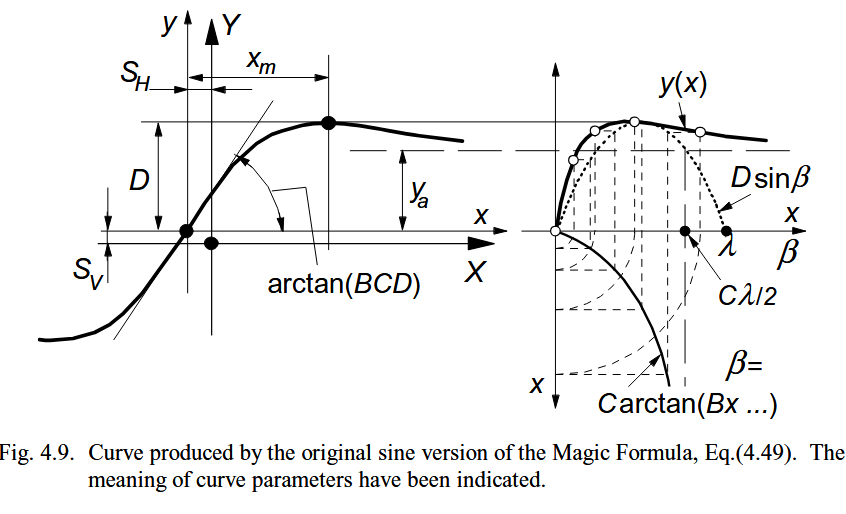
上图通过典型的侧向力特性曲线阐释了部分参数的含义。显然，系数 $D$ 代表峰值（相对于中心 $x$ 轴且当 $C=1$ 时），而乘积 $BCD$ 对应原点处（$x=y=0$）的斜率。形状因子 $C$ 控制公式 $(1)$ 中正弦函数的范围极限，从而决定最终曲线的形状。因子 $B$ 用于确定原点处的斜率，故称为刚度因子。因子 $E$ 则用于控制峰值处的曲率，同时决定峰值的水平位置。

相似性方法

魔术公式是基于轮胎试验数据拟合得到的，试验的变量包括垂向载荷、轮胎路面摩擦系数工况等等，不同的条件对应不同的公式参数。而在车辆行驶过程中，轮胎的垂向载荷变化幅度与频率较大，单一的一套参数无法应对复杂多变的车辆工况。

因此，为模拟轮胎在不同路面的行为，采用相似性方法。该方法在保持小滑移量线性行为的同时，可预测极限剪切力的变化。

当已知轮胎测量值的摩擦系数 $\mu_0$ 与模拟工况的摩擦系数 $\mu$ 时，魔术公式 $(1)$ 的函数按以下方式修正：

$$y=\dfrac{\mu}{\mu_0} \dfrac{F_z}{F_{z0}} y(\dfrac{\mu_0}{\mu}x) \tag{3}$$

其本质是基于曲线形状的相似模拟，该方法通过引入无量纲比例因子，用一套在“参考工况”下标定的核心参数，经数学缩放来高效预测其他工况下的轮胎力，从而在保证模型精度的同时，避免了为海量工况组合逐一进行昂贵试验的不可行性，平衡了工程实用性与经济性。

相似性方法通过引入无量纲比例因子，

组合理论

定义纵侧向的理论滑移量为：

$$\begin{aligned} &\sigma_x = \dfrac{\kappa}{1+\kappa} \\ &\sigma_y = \dfrac{\tan \alpha}{1+\kappa} \end{aligned} \tag{4}$$

则总理论滑移率为

$$\sigma^* = \sqrt{\sigma_x^2 + \sigma_y^2} \tag{5}$$

于是可以得到在组合滑移工况下的魔术公式

$$F_x = \dfrac{\sigma_x}{\sigma^*}F_{x0}(\sigma^*/\mu)\quad,\quad F_y = \dfrac{\sigma_y}{\sigma^*}F_{y0}(\sigma^*/\mu) \tag{6}$$

其中，$F_{x0},F_{y0}$ 为纯滑移工况下的纵侧向力。

最终形式

结合上述理论及公式 $(1)(3)(6)$，最终魔术公式为：

$$\begin{cases} F_x = \dfrac{\sigma_x}{\sigma^*} \dfrac{\mu}{\mu_0} \dfrac{F_z}{F_{z0}} D_{x0} \sin [C_{x0} \arctan\{B_{x0} \sigma^*/\mu-E_{x0}(B_{x0} \sigma^*/\mu-\arctan B_{x0}\sigma^*/\mu)\}] \\\\ F_y = \dfrac{\sigma_y}{\sigma^*} \dfrac{\mu}{\mu_0} \dfrac{F_z}{F_{z0}} D_{y0} \sin [C_{y0} \arctan\{B_{y0} \sigma^*/\mu-E_{y0}(B_{y0} \sigma^*/\mu-\arctan B_{y0} \sigma^*/\mu)\}] \\ \end{cases} \tag{7}$$

横纵向坐标的偏移 $S_V,S_H$根据实际情况增加或删去，本文采用无偏移的假设。

不过，值得注意的是，其中$D_{x0,y0} = \mu_{0} F_{z0} \xi_{x,y}$，$\xi$ 是拟合参数。$D_{x0,y0}$ 代入后可以抵消基准参数 $\mu_0,F_{z0}$，因此用于计算的魔术公式一般为：

$$\begin{cases} F_x = \dfrac{\sigma_x}{\sigma^*} \mu F_z \xi_x \sin [C_{x0} \arctan\{B_{x0} \sigma^*/\mu-E_{x0}(B_{x0} \sigma^*/\mu-\arctan B_{x0}\sigma^*/\mu)\}] \\ \\ F_y = \dfrac{\sigma_y}{\sigma^*} \mu F_z \xi_y \sin [C_{y0} \arctan\{B_{y0} \sigma^*/\mu-E_{y0}(B_{y0} \sigma^*/\mu-\arctan B_{y0} \sigma^*/\mu)\}] \\ \end{cases} \tag{8}$$

Calibrated

版权所有

版权归属：Duangce

许可证：署名 4.0 国际 (CC-BY-4.0)