线控转向系统Simulink建模
上一节的分析结果是两组用微分方程描述的线控转向系统动力学模型。在此基础上可以开展Simulink建模工作。（当然Simulink只是建模仿真工具之一，使用C/C++、Python等语言也可以开发模型并进行数值仿真，但是Simulink能够提供稳定的仿真流，使建模工作仅需重点关注模型而不必为设计复杂的仿真流而浪费过多时间，因此具有快速实现的特点。）
其他阅读：Simulink提供了多种建模方式，包括使用状态空间State-space，mat函数Matlab Function，simulink基础模块，传递函数Transfer Fcn。详情请见文末[其他阅读]。
Simulink 建模
方向盘总成
上节所建立的方向盘总成的动力学模型为：
方向盘总成的模型与执行器较为相似，可以参考以下执行器总成的建模。
执行器总成
根据上一节的结论，执行器的动力学微分方程组为：
Simulink的建模完全依赖于微分方程组，首先分析该方程组中的所有变量，这些变量可分为参数变量、状态变量、输入量。参数变量包括，状态变量包括及其各阶导数，输入量包括。而根据摩擦力模型，摩擦力是上述状态变量导数的函数。将每个状态量的最高阶导数放在等式的左边，可以得到：
如此，在等式右边的方括号内的所有项都可以使用一个simulink add模块组合起来，这是建模的关键。方括号内容除了已知参量、外部输入，就是与状态量相关的量，这些变量可以通过对状态变量的最高阶导数积分后，乘以相对应的系数得到。而状态变量的最高阶导数在等式左边，即为simulink add模块的输出除以一个质量/惯量系数。由此，可以建立模型如下图所示：
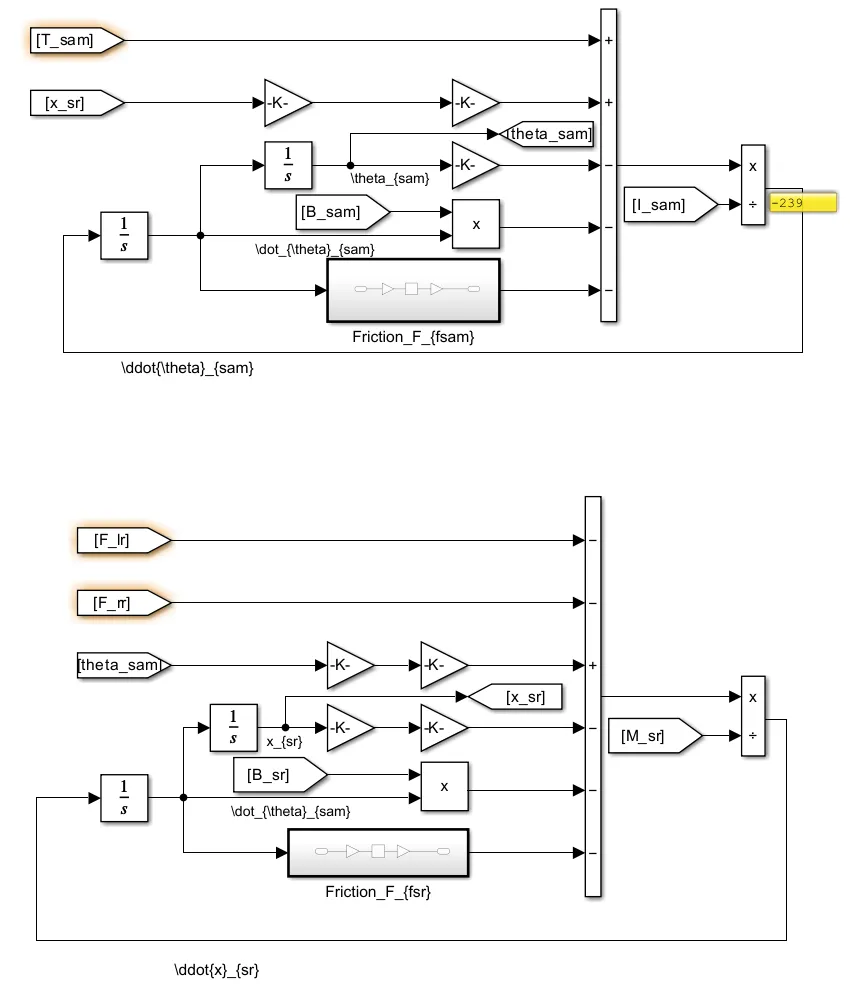
简单仿真，齿条位移结果如下：
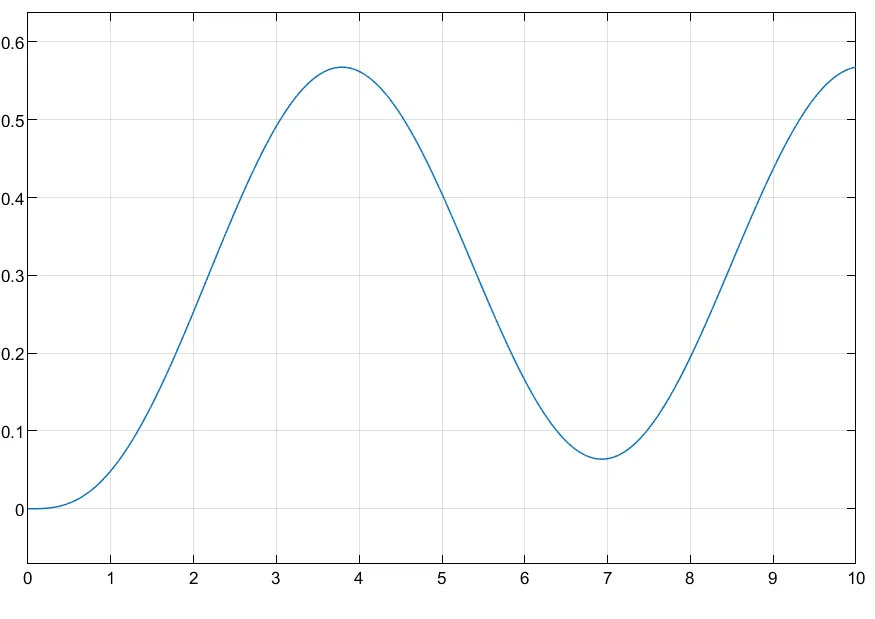
模型验证
在完成模型搭建的工作后，必须要进行的工作是对模型进行验证，以确保模型的有效性。验证的方式就是与更加可信的数据进行对比，例如在动力学建模研究中常与CarSim仿真结果进行对比，比较二者在相同输入下的仿真输出结果（即系统状态）。当然也可以与实车实验的结果进行对比，但是这样的工作量较大，并且CarSim具有较高的可信度，因此通过实车实验进行模型验证不宜用在非专攻的动力学建模研究中。
通过CarSim进行模型验证，核心在于保持CarSim模型与Simulink模型在相同条件下进行仿真，必须保证二者的唯一区别为系统动力学模型的载体，而系统的输入、系统的结构参数等，必须保持一致，这样的对比才有意义。其中，转向系统模型验证的难点在于如何设置参数保证两个不同模型的参数一致性，CarSim的转向系统没有线控转向，因此部分参数须特别设置，并且CarSim转向系统参数设置页面的参数与Simulink模型的参数如何对应，也同样需要逐一确认，相当耗时。
一些模型验证结果如下，分别测试了转向电机正弦输入（大/小力矩）、阶跃输入三个工况：
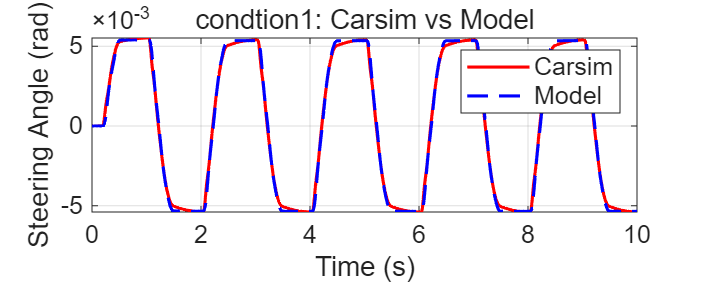
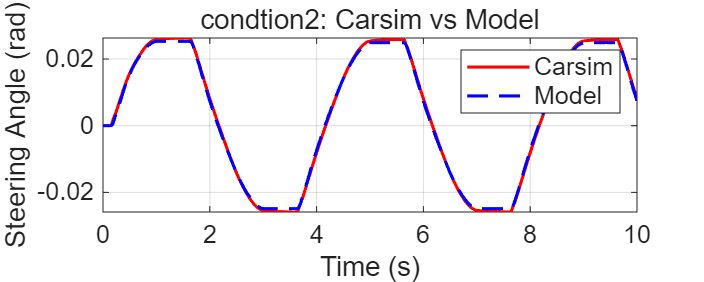
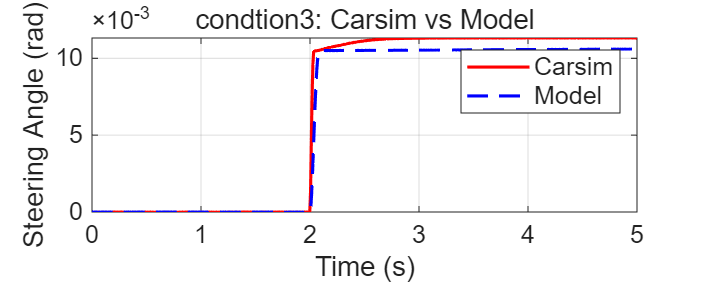
验证时，如何设置，如何操作等相关细节：loading......
其他阅读（未完待续）
前文提到“Simulink提供了多种建模方式，包括使用状态空间State-space，mat函数Matlab Function，simulink基础模块，传递函数Transfer Fcn“，下面将首先对每种建模方式的特点进行总体上的分析，再通过建模、仿真、对比以提供佐证。
在Simulink中使用State-space状态空间法建模会增大计算量，其时间复杂度约为,为状态变量的维度。使用状态空间描述被控对象是现代控制的经典方法，使用矩阵代替微分方程组有助于简化在系统性能分析、控制器设计等方面的复杂计算。但是由于其涉及矩阵运算，特别是积分等复杂运算，所以会耗费过多的时间，因此在高维模型中不宜使用该方法建模。