前言

三自由度平面运动模型描述的是车辆的纵向运动、侧向运动、横摆运动。该模型的所有力都可以在一个车辆俯视图中画出来，因此该模型相较于3自由度的操纵-侧倾模型更简单。由于其在模型复杂度与精度之间具有良好的平衡，该模型被广泛应用于车辆操纵稳定性分析、车辆状态估计、自动驾驶路径跟踪控制以及车辆动力学控制系统设计等研究与工程实践中。

本节将从动力学角度出发逐步推导该模型的动力学微分方程，并且给出状态空间方程。当然，也可以使用拉格朗日法从能量角度出发建模。

一、动力学建模

符号对照表

同样首先进行物理设定及符号约定。坐标系仍为在 整车模型概述 中提到的 ISO 车辆坐标系。符号约定则如下所示：

符号	物理意义	单位
$m$	整车质量	kg
$I_z$	车辆绕z轴的转动惯量	kg·m²
$l_f$	质心至前轴距离	m
$l_r$	质心至后轴距离	m
$v_x, v_y$	质心纵向、侧向速度	m/s
$r$	横摆角速度	rad/s
$\delta_f$	前轮转角	rad
$F_{xf}, F_{xr}$	前、后轴纵向力	N
$F_{yf}, F_{yr}$	前、后轴侧向力	N
$α_f, α_r$	前、后轮胎侧偏角	rad
$κ_f, κ_r$	前、后轮胎纵向滑移率	-

基本动力学方程

纵向、侧向、横摆平衡：

$$\begin{aligned} m a_x = \sum F_x,\\ m a_y = \sum F_y,\\ I_z \dot{r} = \sum M_z. \end{aligned} \tag{1}$$

据 整车不得不说的事的推导可知：

$$\begin{cases} a_x = \dot v_x - v_y r,\\ a_y = \dot v_y + v_x r. \end{cases} \tag{2}$$

图 1 3DOF平面动力学模型

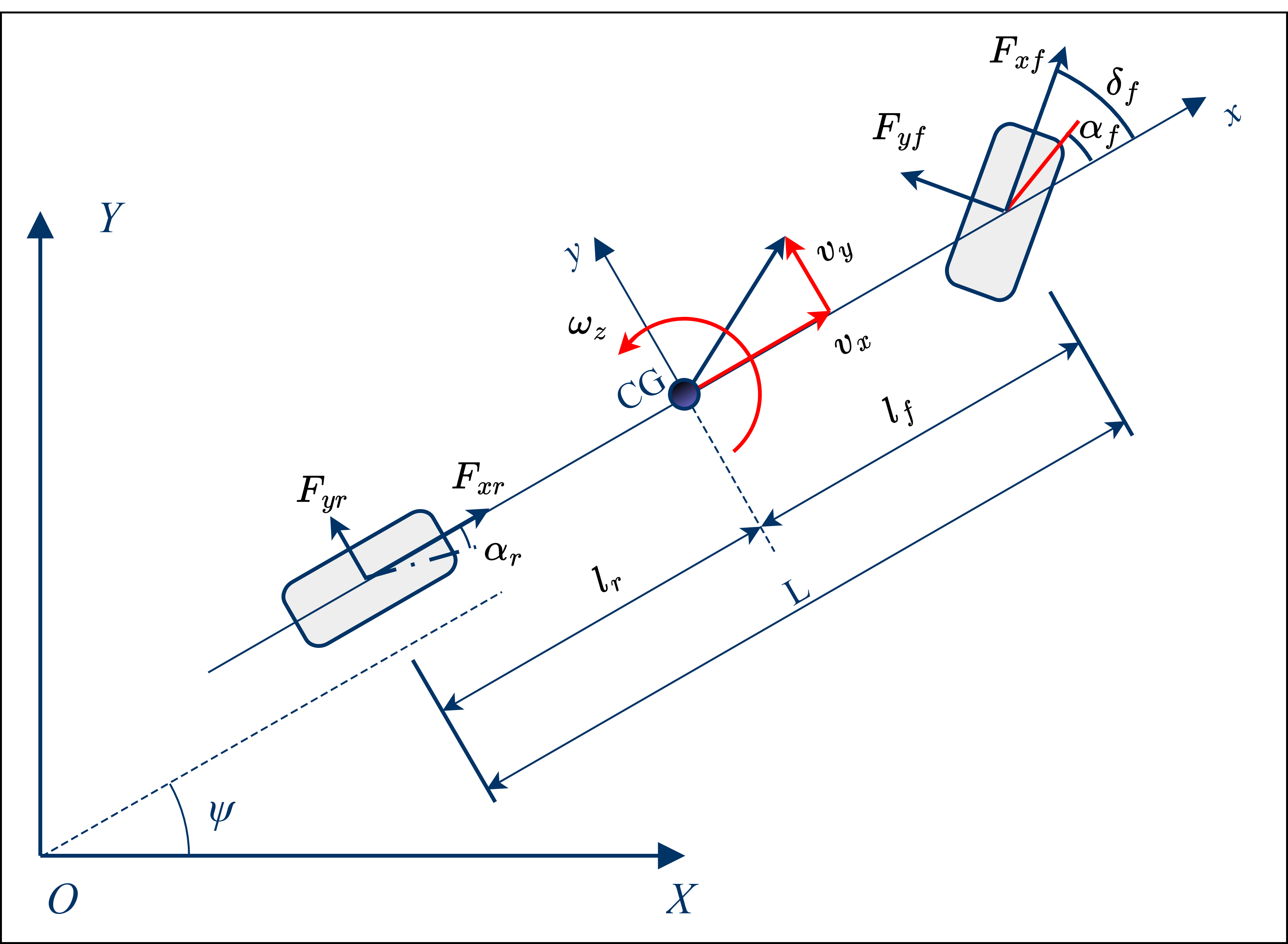
根据上示的模型受力图可知，整车在纵向、侧向、横摆的受力合分别为：

$$\begin{cases} \sum F_x = F_{xf} \cos \delta_f - F_{yf} \sin \delta_f + F_{xr},\\ \sum F_y = F_{xf} \sin \delta_f + F_{yf} \cos \delta_f + F_{yr},\\ \sum M_z = l_f (F_{xf} \sin \delta_f + F_{yf} \cos \delta_f) - l_r F_{yr}. \end{cases} \tag{3}$$

因此，结合上式(1)(3)，可以得到描述整车纵向、侧向、横摆运动的微分方程组：

$$\begin{cases} ma_x = F_{xf} \cos \delta_f - F_{yf} \sin \delta_f + F_{xr},\\ ma_y = F_{xf} \sin \delta_f + F_{yf} \cos \delta_f + F_{yr},\\ I_z \dot r= l_f (F_{xf} \sin \delta_f + F_{yf} \cos \delta_f) - l_r F_{yr}. \end{cases} \tag{4}$$

此外，可以结合上三式(1)(2)(3)，以$(v_x,v_y,r)$为状态变量进行整理，得到如下的微分方程组：

$$\begin{cases} \begin{aligned} \dot{v}_x &= v_y r + \frac{1}{m} \left[ F_{xf} \cos \delta_f - F_{yf} \sin \delta_f + F_{xr} \right], \\ \dot{v}_y &= -v_x r + \frac{1}{m} \left[ F_{xf} \sin \delta_f + F_{yf} \cos \delta_f + F_{yr} \right], \\ \dot{r} &= \frac{1}{I_z} \left[ l_f (F_{xf} \sin \delta_f + F_{yf} \cos \delta_f) - l_r F_{yr} \right]. \end{aligned} \end{cases} \tag{5}$$

其中，轮胎力可以是非线性函数，也可以进行线性化，本节使用非线性轮胎模型，即 轮胎数学模型中介绍的魔术公式轮胎模型MF，轮胎力表示为：

$$\begin{aligned} F_{xf} &= f_{xf}(\kappa_f,\, \alpha_f(\delta_f, v_x, v_y, r),\, F_{zf}), \\ F_{yf} &= f_{yf}(\kappa_f,\, \alpha_f(\delta_f, v_x, v_y, r),\, F_{zf}), \\ F_{xr} &= f_{xr}(\kappa_r,\, \alpha_r(v_x, v_y, r),\, F_{zr}), \\ F_{yr} &= f_{yr}(\kappa_r,\, \alpha_r(v_x, v_y, r),\, F_{zr}). \end{aligned} \tag{6}$$

根据 轮胎：合纵连横 中的介绍可以基于车速及轮速计算轮胎的滑移率$\kappa$，基于车速、横摆角速度、车轮转角计算各轮的侧偏角$\alpha$，再将结果代入上式(6)可以计算得到最终的轮胎力，由此可以建立整车非线性的三自由度平面运动模型。

二、 one more

模型的非线性特性主要来源于两个方面：运动学耦合项 $v r$, $u r$；轮胎力非线性函数 $f_{xf}$, $f_{yf}$ 等。

此外，此模型为“自行车模型”，未考虑左右轮载荷转移及对应的轮胎特性变化。若要更高精度，需扩展至双轨模型，将前/后轴轮胎力按照左右轮胎分开，并引入垂直载荷的动态计算。

版权所有

版权归属：Duangce

许可证：署名 4.0 国际 (CC-BY-4.0)