线控转向系统的数学模型描述了该系统的行为规律，也就是系统输入、状态、输出之间的因果关系及其物理机制。数学模型，其一可用于分析系统性能，包括稳定性、响应速度、频率特性等；其二可以用于仿真验证，使用计算机模拟实际工况并计算系统的响应，实现预开发从而降低成本；其三还可以用于设计控制器，基于模型的控制，如模型预测控制、滑模控制、线性二次型调节器等都需要基于模型进行控制器设计。数学模型作为通用语言，能够使机械、电控、软件等多个领域的工程师能够协同开发。 一般机械系统有运动学模型和动力学模型，前者从几何角度描述了被研究对象的运动，不涉及力与质量，后者则考虑引起运动的力与力矩，其描述了力或力矩引起物体运动状态变化的机理。可以说，运动学模型是动力学模型的基础，但是本文并不打算从线控转向系统的运动学模型扩展出动力学模型。而是首先再次讨论线控转向系统的机械结构并进行必要的简化，其次基于简化系统，使用牛顿-欧拉法建立其动力学模型；最后在文末论述如何基于动力学模型推导出动力学模型，并且给出其逆运动学模型。

物理架构

线控转向系统主要由三部分组成：方向盘总成、电子控制单元ECU、转向执行总成。 方向盘总成主要由方向盘、转向管柱、路感电机、减速器等组成，其空间布置关系如下图所示。

图 1 SBW系统结构示意图

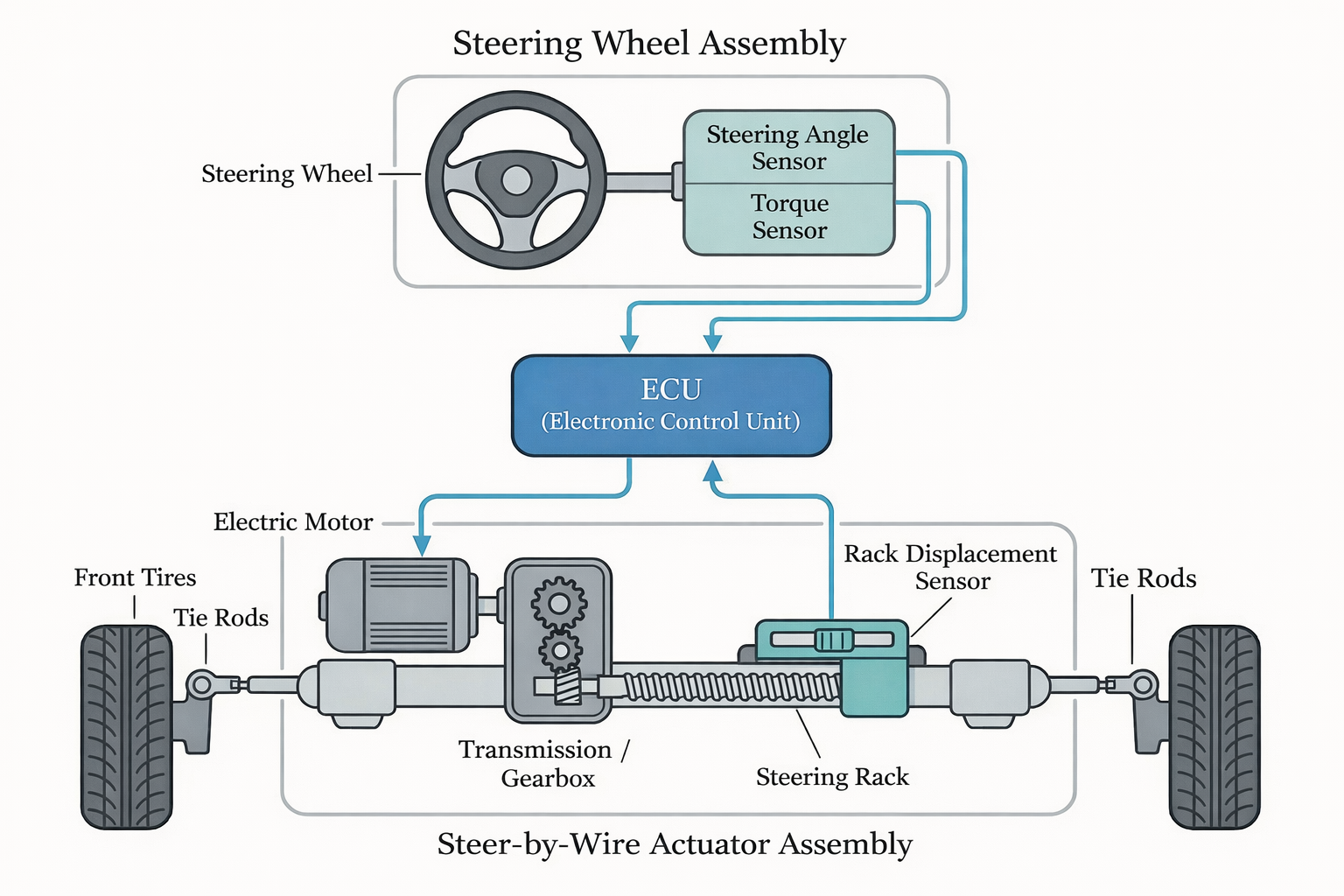
减速器一般为蜗轮蜗杆或行星齿轮。 电子控制单元通过线缆与外设进行信号交换，是实现线控的基础与关键。由于信号传递与信息处理一定时间，因此ECU可以建模为一定的时滞/延迟环节 Delay. 转向执行总成主要由转向电机、减速器、齿条、转向拉杆节臂等组成，轮胎不是狭义的转向系统的一部分，但是它是转向系统的作用对象，其侧偏力的生成与转向系统密切相关，因此在转向系统建模时通常会一并考虑。

因此，一般转向系统的动力学建模，主要考虑转向系统的方向盘总成、电子控制单元的动力传递链路。首先根据实际设计需求，对动力学系统做一定的简化，例如将刚性连接的部分视为一个整体；其次，根据动力传动链路，依次建立各质量体的动力学微分方程；最后整理微分方程得到最终的动力学模型。 此外，由于整车动力学控制一般计算最优的车轮转角，因此需要我们根据期望车辆转角计算出对应的期望电机转角，此时就需要使用到逆运动学模型，其实就是求电机转角与车轮转角之间的关系。根据转向梯形可以计算出车轮转角和齿条位移之间的关系（这是非线性的），根据减速器传动比可以计算出齿条位移与转向电机转角之间的关系，从而可以构建逆运动学模型，当然它是非线性的。在实际使用中，常见的非线性逆运动学模型可以通过表格、拟合公式等进行表示。

动力学建模

动力学系统所受力一般可以分为：驱动力、负载力、惯性力、阻尼力、摩擦力。本节将依照该受力分析思路，进行动力学建模。摩擦力模型

方向盘总成

方向盘与转向管柱刚性连接，因此将其视为一个整体进行分析。减速器刚度较高，因此减速器的输入与输出之间的关系可以通过传动比直接构建。路感电机的输出轴受电磁驱动，并负载减速器力矩。方向盘与转向管柱、路感电机输出轴建模如下：

数学严谨的建模

考虑到旋转体两端的动态差异，则可以建立如下的双端平均模型。 对方向盘受力分析，其动力学微分方程可以表示为：

$$I_{hw} (\ddot{\theta}_{hw} + \ddot{\theta}_{rgout})/2 + B_{hw} (\dot{\theta}_{hw} + \dot{\theta}_{rgout})/2 + F_{fhw} = T_{hw} + T_{rgout}$$

其中，$I_{hw},B_{hw},F_{fhw}$分别为转向盘及转向管柱的转动惯量、阻尼系数、摩擦力矩，$\theta_{hw},\theta_{rgout}$分别为转向盘的转角、减速器输出处转角，$T_{hw}$为驾驶员对方向盘所施力矩，$T_{rgout}$为减速器对转向管柱所施力矩，其满足：

$$(T_{hw} - T_{rgout})/2 = k_{hw}(\theta_{hw}-\theta_{rgout})$$

其中，$k_{hw}$为转向盘及转向管柱的扭转刚度。

对路感电机受力分析，其动力学微分方程可以表示为：

$$I_{rm} (\ddot{\theta}_{rm} + \ddot{\theta}_{rgin})/2+ B_{rm} (\dot{\theta}_{rm} +\dot{\theta}_{rgin})/2 + F_{frm} = T_{rm} - T_{rgin}$$

其中，$I_{rm},B_{rm},F_{frm}$分别为路感电机输出轴的转动惯量、阻尼系数、摩擦力矩，$\theta_{rm},\theta_{rgin}$分别为路感电机的电磁转角、减速器输入端的转角，$T_{rm}$为电磁驱动力矩，$T_{rgin}$为减速器输入扭矩。其中减速器转角与力矩的状态量满足：

$$\theta_{rgin} = i_{gh} \theta_{rgout}\\ T_{rgin} = i_{gh} T_{rgout}$$

其中，$i_{hg}$为方向盘总成的减速器减速比。

结合上式，可得：

$$\left\{ \begin{aligned} &I_{hw} (\ddot{\theta}_{hw} + \ddot{\theta}_{rgout})/2 + B_{hw} (\dot{\theta}_{hw} + \dot{\theta}_{rgout})/2 + F_{fhw} = T_{hw} + T_{rgout}\\ &(T_{hw} - T_{rgout})/2 = k_{hw}(\theta_{hw}-\theta_{rgout})\\ &I_{rm} (\ddot{\theta}_{rm} + \ddot{\theta}_{rgin})/2+ B_{rm} (\dot{\theta}_{rm} +\dot{\theta}_{rgin})/2 + F_{frm} = T_{rm} - T_{rgin}\\ &(T_{rm} - T_{rgin})/2 = k_{rm}(\theta_{rm} - \theta_{rgin})\\ &\theta_{rgin} = -i_{gh} \theta_{rgout}\\ &T_{rgin} = i_{gh} T_{rgout} \end{aligned} \right.$$

面向工程应用的建模

上述模型虽然在数学上更加严谨，但是其中参数的辨识难度高、计算复杂度高，适用于高保真的动态特性建模，而不适用于控制算法的设计，因此给出如下的单体建模方法： 对于方向盘：

$$I_{hw} \ddot{\theta}_{hw} + B_{hw} \dot{\theta}_{hw} + F_{fhw} = T_{hw} - T_{rgout}$$

其中，$I_{hw},B_{hw},F_{fhw}$分别为转向盘及转向管柱的转动惯量、阻尼系数、摩擦力，$\theta_{hw}$为转向盘的转角，$T_{hw}$为驾驶员对方向盘所施力矩，$T_{rgout}$为减速器对转向管柱所施力矩，其满足：

$$T_{rgout} = k_{gh}(\theta_{hw}-\theta_{rgout})$$

其中，$k_{gh}$为转向盘及转向管柱的扭转刚度，$\theta_{rgout}$为转向管柱在减速器处的转角。

对路感电机受力分析，其动力学微分方程可以表示为：

$$I_{rm}\ddot{\theta}_{rm} + B_{rm}\dot{\theta}_{rm} + F_{frsm} = T_{rm} - T_{rgin}$$

其中，$I_{rm},B_{rm},F_{frsm}$分别为路感电机输出轴的转动惯量、阻尼系数、摩擦力，$\theta_{rm}$为路感电机的转角，$T_{rm}$为电磁驱动力矩，$T_{rgin}$为方向盘总成减速器对电机所施力矩，其满足：

$$T_{rgin} = k_{gm}(\theta_{rm}-\theta_{rgin})$$

其中，$k_{gm}$为路感电机输出轴的扭转刚度，$\theta_{rgin}$为路感电机输出轴在减速器处的转角。

设减速器输入与输出端的电机输出轴转角、转向管柱转角分别为$\theta_{rgin},\theta_{rgout}$，由于减速器刚度较高，因此假设其输入输出之间无弹性变形差异，即：

$$\theta_{rgin} = i_{gh} \theta_{rgout}\\ T_{rgout} = -i_{gh} T_{rgin}$$

其中，$i_{gh}$为方向盘总成减速器的减速比。 结合上式，可得：

$$\left\{ \begin{aligned} &I_{hw} \ddot{\theta}_{hw} + B_{hw} \dot{\theta}_{hw} + F_{fhw} = T_{hw} - T_{rgout}\\ &I_{rm}\ddot{\theta}_{rm} + B_{rm}\dot{\theta}_{rm} + F_{frsm} = T_{rm} - T_{rgin}\\ &T_{rgout} = k_{gh}(\theta_{hw}-\theta_{rgout})\\ &T_{rgin} = k_{gm}(\theta_{rm}-\theta_{rgin})\\ &\theta_{rgin} = i_{gh} \theta_{rgout}\\ &T_{rgout} = -i_{gh} T_{rgin} \end{aligned} \right.$$

该模型的计算仍然较为复杂，由于电机输出轴扭转刚度较大，假设其为刚性部件，则$\theta_{rm} = \theta_{rgin}$，由此将上述模型简化得到：

$$\left\{ \begin{aligned} &I_{hw} \ddot{\theta}_{hw} + B_{hw} \dot{\theta}_{hw} + F_{fhw} = T_{hw} - k_{gh}(\theta_{hw}-\theta_{rm}/i_{gh})\\ &I_{rm}\ddot{\theta}_{rm} + B_{rm}\dot{\theta}_{rm} + F_{frsm} = T_{rm} - k_{gh}(\theta_{rm}/i_{gh}-\theta_{hw})/i_{gh}\\ \end{aligned} \right.$$

转向执行总成

转向执行总成包括转向电机、减速器、转向齿条、拉杆等。转向执行总成与方向盘总成的动力学模型大同小异，主要区别在于：转向齿条为直线运动，方向盘及转向管柱为旋转运动。

对于转向电机：

$$I_{sam}\ddot{\theta}_{sam} + B_{sam} \dot{\theta}_{sam} + F_{fsam} = T_{sam} - T_{bin}$$

其中，$I_{sam},B_{sam},F_{fsam}$分别为转向执行电机输出轴的转动惯量、阻尼系数、摩擦力，$\theta_{sam}$为其转角，$T_{sam}$为电磁驱动力矩，$T_{bin}$为滚珠丝杠减速器（或其他减速器）对电机输出轴作用力矩，其满足：

$$T_{bin} = k_{bm}(\theta_{sam}-\theta_{bin})$$

其中，$k_{bm}$为转向执行电机输出轴的扭转刚度，$\theta_{bin}$为该电机输出轴在减速器处的转角。假设减速器输入输出稳定，即：

$$\theta_{bin} = i_{bs} x_{sr}$$

对于转向齿条：在转向过程中，齿条受到电机通过滚珠丝杠副对其施加的驱动力，同时受到拉杆对其在水平直线运动方向上的阻力。因此：

$$M_{sr}\ddot{x}_{sr} + B_{sr}\dot{x}_{sr} + F_{fsr} = F_{bout} + F_{lr} + F_{rr}$$

其中，$M_{sr},B_{sr},F_{fsr}$分别为转向齿条的质量、阻尼系数、摩擦力，$x_{sr}$为齿条位移，$F_{lr},F_{rr}$分别为拉杆对齿条的转向阻力在齿条位移方向上的分力，$F_{bout}$为减速器对齿条作用力，其满足：

$$T_{bin} = F_{bout}/i_{bs}$$

其中，$i_{bs}$为转向执行总成的减速比。

整理上述公式可得：

结合上式，可得：

$$\left\{ \begin{aligned} &I_{sam}\ddot{\theta}_{sam} + B_{sam} \dot{\theta}_{sam} + F_{fsam} = T_{sam} - T_{bin}\\ &M_{sr}\ddot{x}_{sr} + B_{sr}\dot{x}_{sr} + F_{fsr} = F_{bout} + F_{lr} + F_{rr}\\ &T_{bin} = k_{bm}(\theta_{sam}-\theta_{bin})\\ &T_{bin} = F_{bout} / i_{bs}\\ &\theta_{bin} = i_{bs} x_{sr} \end{aligned} \right.$$

可以进一步整合：

$$\left\{ \begin{aligned} &I_{sam}\ddot{\theta}_{sam} + B_{sam} \dot{\theta}_{sam} + F_{fsam} = T_{sam} - k_{bm}(\theta_{sam}-i_{bs}x_{sr})\\ &M_{sr}\ddot{x}_{sr} + B_{sr}\dot{x}_{sr} + F_{fsr} = i_{bs}k_{bm}(\theta_{sam}-i_{bs}x_{sr}) + F_{lr} + F_{rr}\\ \end{aligned} \right.$$

版权所有

版权归属：Duangce

许可证：署名 4.0 国际 (CC-BY-4.0)