电子机械制动数学模型
约 3198 字大约 11 分钟
2026-01-03
一、前言
二、EMB系统结构与原理
如前文所述,在车辆行驶过程中,EMB是直接使用电机经机械传动装置直接驱动制动块,使其与制动盘紧密贴合产生摩擦力,使车轮减速;减速的车轮与路面产生相对运动,即纵向滑移率,并且此时的滑移率产生与行驶方向相反的制动力,从而制动汽车。
电子机械制动系统如下图所示,该系统主要分为电子踏板模块,ECU模块,制动执行模块三部分,其中电子踏板模块不仅需要采集输入信号,还需要实现踏板力模拟;ECU模块主要涉及通讯与控制算法设计;制动执行模块是一条从电机至轮胎制动盘的运动/动力传递链路。
2.1 电子踏板模块
电子踏板模块主要由踏板机械总成、踏板感模拟器以及多重冗余的传感器组构成。作为驾驶员与制动系统之间的人机交互接口,电子踏板模块在结构上彻底取消了与制动主缸的机械连接,实现了完全的物理解耦。其中,踏板感模拟器通常采用弹簧与阻尼器的组合机构,旨在复现传统液压制动踏板在不同行程下的力-位移迟滞特性,确保驾驶员获得熟悉的脚感反馈。
电子踏板模块的核心任务是将驾驶员的制动意图转化为高精度的数字电信号。当驾驶员踩下踏板时,集成的位移传感器或角度传感器实时采集踏板的行程与运动速率,并将这些物理量转换为电信号。与此同时,踏板模拟器根据预设的力学模型产生相应的反作用力,为驾驶员提供触觉反馈。经过校验后的信号通过车载通信网络传输至控制单元,作为计算目标制动力矩的基础输入,从而实现制动意图的精准传递。
2.2 电子控制单元
电子控制单元是EMB系统的决策与算力核心,其硬件架构需满足极高的功能安全等级要求。该模块通常集成高性能的双核微控制器、电源管理电路以及功率驱动电路。为了确保系统的可靠性,ECU内部采用双路冗余设计,并配备CAN-FD或FlexRay等高速通信接口,以便与整车域控制器及各轮端执行器进行实时数据交互与指令下发。
ECU模块接收来自电子踏板的意图信号及轮速、横摆角速度等车辆状态信号,实时解算出各车轮所需的目标夹紧力。随后,ECU通过脉宽调制(PWM)技术控制功率驱动电路,向电机输出精确的电压矢量。此外,该模块还持续运行系统诊断程序,实时监测传感器与执行器的健康状态,一旦检测到故障,立即切换至安全备份模式,确保车辆在紧急工况下的制动安全性。
2.3 制动执行模块
制动执行模块主要包含高功率密度的电机、减速增矩传动机构以及车轮。常见的制动电机为无刷直流电机与永磁同步电机;常见的传动机构配置为多级行星齿轮减速器配合滚珠丝杠或行星滚柱丝杠,这种设计能够在有限的空间内实现扭矩的放大与运动形式的转换,以承受极大的轴向载荷;车轮中常见的制动装置为盘式制动器。
该模块的工作原理是将电能直接转化为机械制动效能。当接收到ECU的驱动指令后,电机转子迅速产生旋转扭矩,该扭矩经过减速机构放大后传递至运动转换机构。丝杠副将旋转运动转化为制动活塞的直线进给运动,进而推动摩擦衬片压紧制动盘。通过精确控制电机的电流与转角,执行模块能够实现制动夹紧力的毫秒级无级调节,并在制动结束后通过电机反转迅速消除残余力矩,实现主动回位。
三、EMB动力学模型
EMB的电子踏板模块主要涉及机械设计相关的内容,与电控相关性较小,而制动执行模块则较为涉及复杂的动力学与电控问题,因此本节主要针对制动执行模块进行建模。制动执行模块可以被分为电机、机械传动、车轮三个部分。
因此,本节将基于下图所示的制动执行模块的机械结构,使用牛顿-欧拉方法分析其中的动力学关系,主要包括制动力传递方程与车轮制动方程。
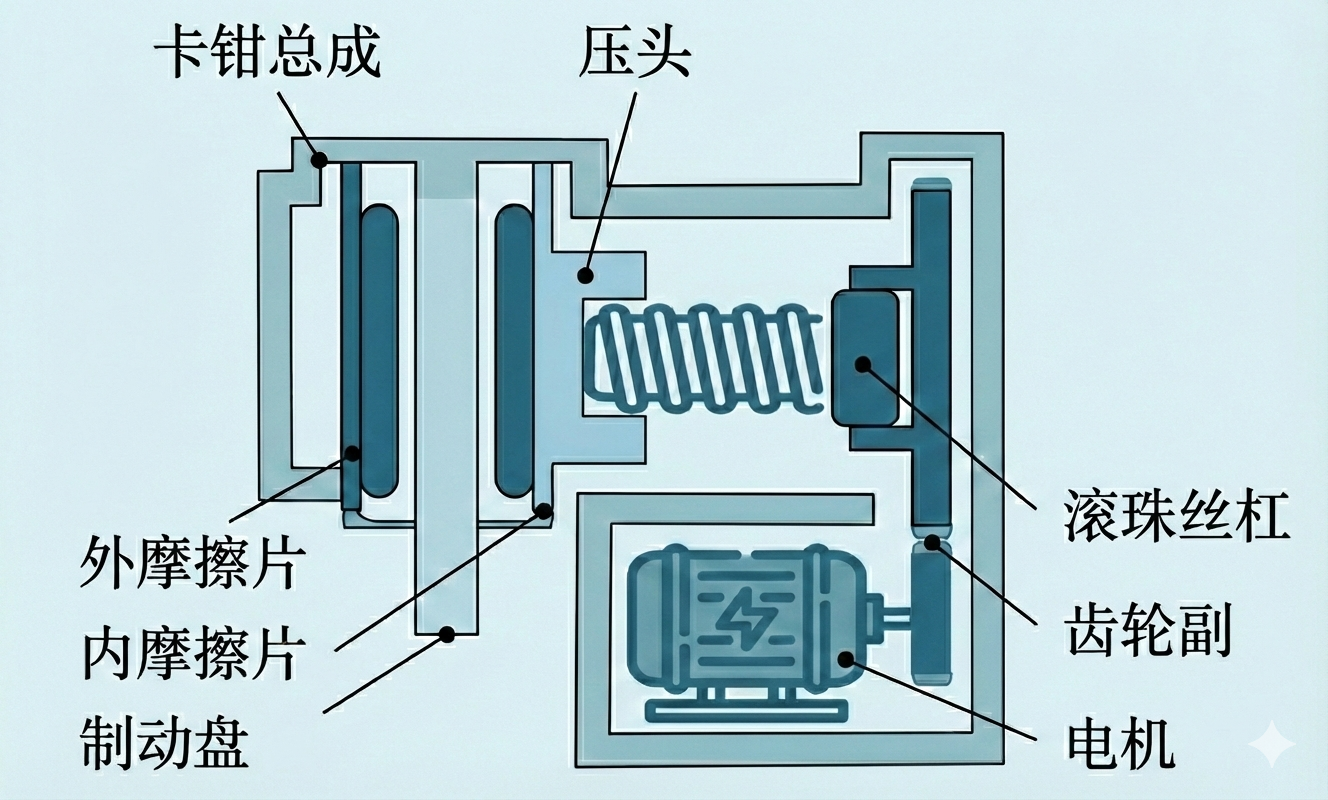
首先给出参数表如下所示。
| 符号 | 物理意义 | 单位 |
|---|---|---|
| iq | 电机 q 轴电流 | A |
| u | 电机驱动电压 | V |
| L | 电机电感 | H |
| R | 电机电阻 | Ω |
| wm | 电机角速度 | rad/s |
| w˙m | 电机角加速度 | rad/s² |
| Jm | 电机转动惯量 | kg·m² |
| km | 电机转矩常数 | N·m/A |
| kw | 反电动势常数 | V·s/rad |
| Te | 电磁转矩(Te=kmiq) | N·m |
| Tf | 摩擦转矩 | N·m |
| Tf0 | 摩擦转矩偏置 | N·m |
| bf | 粘性摩擦系数 | N·m·s/rad |
| Ts | 静摩擦转矩(粘着阈值) | N·m |
| TL | 负载转矩(制动负载) | N·m |
| Fcl | 制动夹紧力 | N |
| γ | 夹紧力相关摩擦系数 | N·m/N |
| kcl | 夹紧力–转矩增益 | m |
| Ph | 滚珠丝杠导程 | m |
| ig | 减速器传动比 | – |
| ηg | 传动效率 | – |
| θm | 电机转角 | rad |
| θg | 制动间隙对应转角阈值 | rad |
| pi,c | 制动过程多项式系数 | N·rad⁻ᶦ |
| pi,r | 释放过程多项式系数 | N·rad⁻ᶦ |
| np | 多项式阶数 | – |
3.1 电机电气与机械动力学模型
EMB系统包括电机电气回路与机械回路,其状态变量为电机电流与角速度:
LdtdiqJmw˙m=u−Riq−kwwm=kmiq−Tf−TL
其中,iq为电机电流;L为电机电感;R为电机电阻;wm为电机角速度;kw为反电动势常数;u为电机驱动电压;Jm为电机转动惯量;km为转矩常数;Tf为摩擦转矩;TL为与制动力相关的负载转矩。其他物理量为状态量或已知参数,而TL,Tf需要进一步建模。
3.1.1 摩擦转矩
摩擦转矩Tf与夹紧力和运动状态密切相关,采用基于转速与转矩条件的分段模型则为:
Tf=⎩⎨⎧(γFcl+Tf0)sign(wm)+bfwm,kmiq−TL,Tssign(wm),wm=0wm=0 & Te<Tswm=0 & Te≥Ts
其中,γ为与夹紧力相关的系数;Tf0为摩擦转矩偏置;bf为粘性摩擦系数;Ts为静摩擦转矩。其中,γ为时变参数。
3.1.2 负载转矩与夹紧力关系
负载转矩通过机械传动链与夹紧力线性相关:
TL=kclFcl,kcl=2πigηgPh
其中,kcl为夹紧力增益,Ph为滚珠丝杠导程、ig为减速比,ηg为传动效率;Fcl代表夹紧力。
3.1.3 夹紧力与制动扭矩
考虑制动与释放过程中的迟滞特性,夹紧力通过电机转角的分段多项式函数进行估计:
Fcl=⎩⎨⎧0,p0,c+∑i=1nppi,cθmi,p0,r+∑i=1nppi,rθmi,θm<θgθm≥θg & wm≥0θm≥θg & wm<0
其中,pi,c/r (i=0,1,…,np)为多项式系数,需要通过预先采集的实验数据进行辨识,np为多项式阶数。
制动扭矩为:
Tb=2μbrbFcl
其中,μb为摩擦块与制动盘之间的摩擦系数,rb为制动盘的有效工作半径。
3.1.4 制动器无车轮模块最终模型
因此,基于上述推导过程,可以将EMB系统描述为如下的非线性动力学方程组:
⎩⎨⎧i˙q=L1(u−Riq−kwwm)w˙m=Jm1(kmiq−Tf−TL)Tf=⎩⎨⎧(γFcl(θm,wm)+Tf0)sign(wm)+bfwm,kmiq−TL,Tssign(wm),wm=0wm=0 & kmiq<Tswm=0 & kmiq≥TsTL=kclFcl(θm,wm),kcl=2πigηgPhFcl=⎩⎨⎧0,p0,c+i=1∑nppi,cθmi,p0,r+i=1∑nppi,rθmi,θm<θgθm≥θg & wm≥0θm≥θg & wm<0Tb=2μbrbFcl
3.2 车轮制动模型
在制动时,车轮受力情况如下所示:
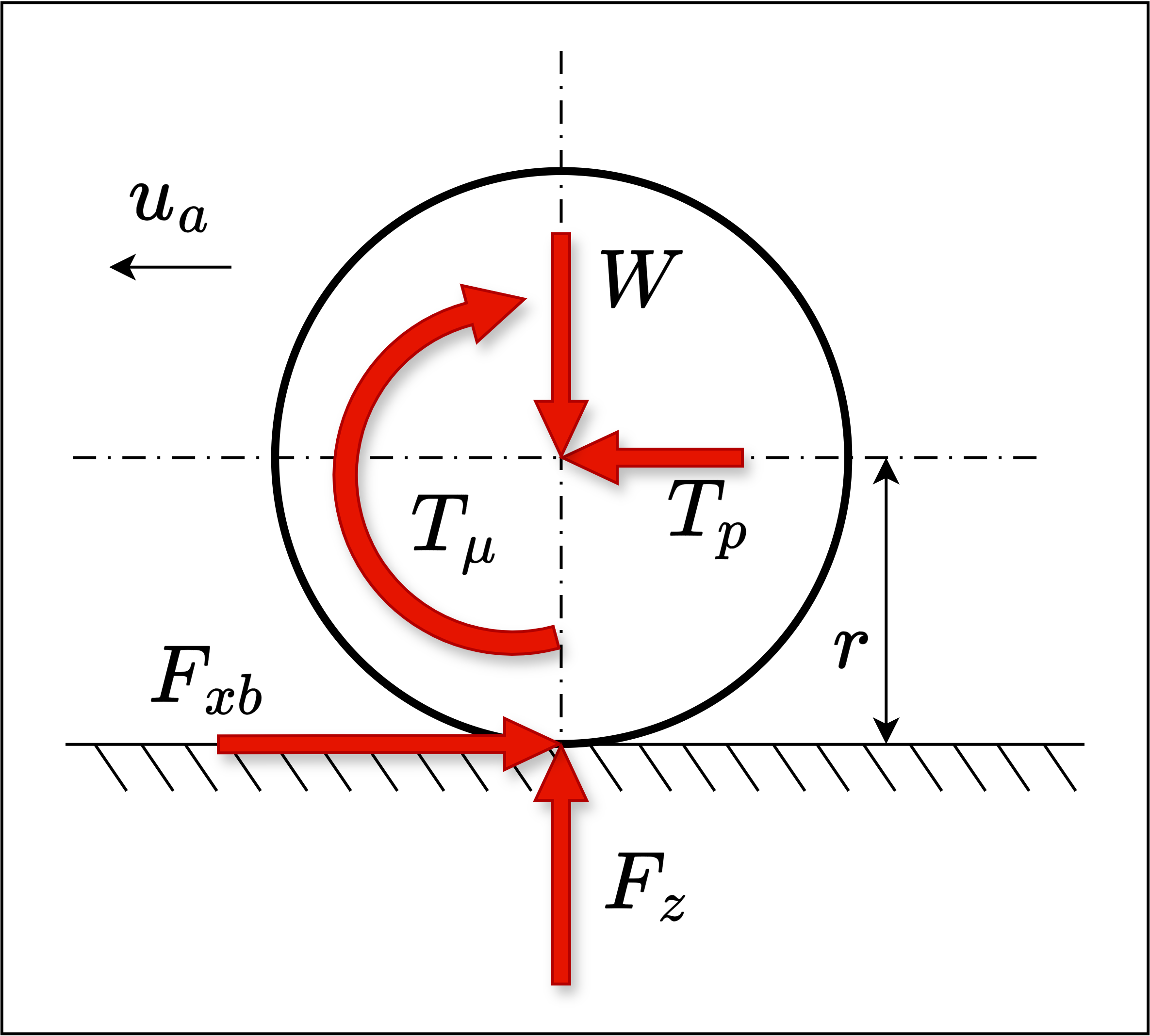
图中,ua指明了车辆前进方向为图示向左方向,W为车轮所受重力,Tb为制动扭矩,Tp是车桥对轮胎的作用力,轮胎反作用力方向相反,阻碍汽车前进,Fxb为车轮所受地面的纵向力,本文为统一表述,在后续使用Fx代替,Fz为路面垂向作用力。
由图可知,影响车轮旋转运动的力主要有制动力矩、路面对轮胎的纵向作用力,车轮的旋转运动动力学方程为:
Jwω˙w=Tb−ReFx
其中,Jw为轮胎绕其旋转运动轴的转动惯量,ω˙w为车轮角加速度,Re为车轮的有效滚动半径,Fx为轮胎所受路面纵向力。
路面对轮胎的纵向作用力Fx可以使用 轮胎数学模型 中所介绍的魔术公式轮胎模型描述,也可以使用如下的简化形式:
Fx=μ(κ)Fz
其中,μ为轮胎路面摩擦系数,是纵向滑移率κ的函数,Fz为轮胎法向载荷。 κ的定义为:
κ=vxReωw−vx
其中,vx为车辆前进速度。
当车辆的仅存在纵向运动时,其轮胎法向载荷为:
Fzfl=Fzfr=(mhlr−mhgv˙x)/(2lf+2lr)Fzrl=Fzrr=(mhlf+mhgv˙x)/(2lf+2lr)
其中,Fzi,i={fl,fr,rl,rr}分别代表左前、右前、左后、右后轮的法向载荷,m为整车质量,lf,lr分别为车辆前后轴至质心的纵向距离,ax为车辆纵向加速度。
3.3 建模假设
最后总结上述建模过程,可以得到如下的建模假设:
- 电机与执行器线性化假设:EMB 中电机的电气与机械行为可由低阶集中参数模型描述,电机转矩与电流呈线性关系,相关参数在工作范围内保持恒定,忽略磁饱和、电磁谐波及功率器件非理想因素。
- 机械传动刚性与线性映射假设:减速器与滚珠丝杠等传动机构被视为刚性系统,其动态效应可用固定增益表示,负载转矩与夹紧力之间满足线性比例关系,不考虑传动间隙、弹性变形及效率随工况变化的影响。
- 摩擦分段切换假设:系统摩擦特性可依据电机转速状态划分为滑动、静止和破粘阶段,各阶段摩擦模型确定,切换条件可由转速符号准确判定。
- 夹紧力确定性映射假设:制动夹紧力在接触阶段可由电机转角唯一确定,制动与释放过程中的迟滞效应可通过分段多项式函数表征,且接触阈值转角固定不变。
- 参数时不变与环境忽略假设:所有模型参数均可通过离线标定获得并长期适用,温度变化、磨损和老化等因素对系统动力学的影响在建模中被忽略。
